
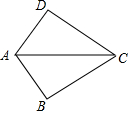
 如图,AB=AD,添加下列一个条件后,仍无法确定△ABC≌△ADC的是( )
如图,AB=AD,添加下列一个条件后,仍无法确定△ABC≌△ADC的是( )| A. | BC=CD | B. | ∠BAC=∠DAC | C. | ∠B=∠D=90° | D. | ∠ACB=∠ACD |
分析 根据全等三角形的判定定理逐个判断即可.
解答 解:A、AB=AD、AC=AC、BC=CD,符合全等三角形的判定定理SSS,能推出△ABC≌△ADC,故本选项不符合题意;
B、AB=AD、∠BAC=∠DAC、AC=AC,符合全等三角形的判定定理SAS,能推出△ABC≌△ADC,故本选项不符合题意;
C、AB=AD、AC=AC、∠B=∠D=90°,符合全等三角形的判定定理HL,能推出△ABC≌△ADC,故本选项不符合题意;
D、AB=AD、AC=AC、∠ACB=∠ACD,不符合全等三角形的判定定理,不能推出△ABC≌△ADC,故本选项符合题意;
故选D.
点评 本题考查了全等三角形的判定定理,能熟记判定定理的内容是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,直角三角形全等还有HL.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A+∠B=180° | B. | ∠B+∠D=180° | C. | ∠B+∠C=180° | D. | ∠A+∠B=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
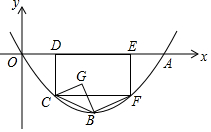 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$ax2-2ax(a>0)与x轴正半轴交于点A,点B是抛物线的顶点,矩形CDEF的顶点D、E在x正半轴上,C、F在抛物线上,且点D的横坐标为1,连结BC、BF,以BC为斜边向右侧作等腰直角三角形BCG
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$ax2-2ax(a>0)与x轴正半轴交于点A,点B是抛物线的顶点,矩形CDEF的顶点D、E在x正半轴上,C、F在抛物线上,且点D的横坐标为1,连结BC、BF,以BC为斜边向右侧作等腰直角三角形BCG查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)(b-a)=a2-b2 | B. | (a-b)2=a2-b2 | ||
| C. | (2x-y)2=4x2-2xy+y2 | D. | (x-2y)(-2y-x)=4y2-x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com