
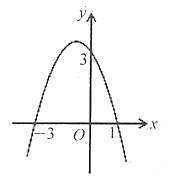
【题目】如图所示是二次函数![]() 的图象,下列结论:
的图象,下列结论:
①二次三项式![]() 的最大值为
的最大值为![]() ;
;
![]() 使
使![]() 成立的
成立的![]() 的取值范围是
的取值范围是![]() ;
;
![]() 一元二次方程
一元二次方程![]() ,当
,当![]() 时,方程总有两个不相等的实数根;
时,方程总有两个不相等的实数根;
![]() 该抛物线的对称轴是直线
该抛物线的对称轴是直线![]() ;
;
![]()
其中正确的结论有______________ (把所有正确结论的序号都填在横线上)
【答案】①③④
【解析】
根据图象求出二次函数的解析式,根据二次函数的性质结合图象可以判断各个小题中的结论是否正确.
由函数图象可知:抛物线过(-3,0),(1,0),(0,3),
∴设抛物线解析式为![]() ,把(0,3)代入得:3=
,把(0,3)代入得:3=![]() ,解得:a=-1,
,解得:a=-1,
∴抛物线为![]() ,即
,即![]() ,
,
∴二次三项式ax2+bx+c的最大值为4,故①正确,
由![]() =3,解得:x=0或x=-2,由图像可知:使y≤3成立的x的取值范围是x≤﹣2或x≥0,故②错误.
=3,解得:x=0或x=-2,由图像可知:使y≤3成立的x的取值范围是x≤﹣2或x≥0,故②错误.
∵二次三项式ax2+bx+c的最大值为4,
∴当k<4时,直线y=k与抛物线![]() 有两个交点,
有两个交点,
∴当k<4时,方程一元二次方程![]() 总有两个不相等的实数根,故③正确,
总有两个不相等的实数根,故③正确,
该抛物线的对称轴是直线x=﹣1,故④正确,
当x=﹣2时,y=4a﹣2b+c>0,故⑤错误.
故答案为:①③④.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
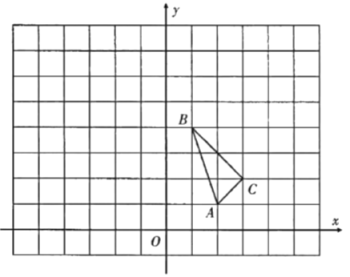
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
请解答下列问题:
(1)画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ,并直接写出
,并直接写出![]() 点的坐标;
点的坐标;
(2)以原点![]() 为位似中心,位似比为1:2,在
为位似中心,位似比为1:2,在![]() 轴的右侧,画出
轴的右侧,画出![]() 放大后的图形
放大后的图形![]() ,并直接写出
,并直接写出![]() 点的坐标;
点的坐标;
(3)如果点![]() 在线段
在线段![]() 上,请直接写出经过(2)的变化后对应点
上,请直接写出经过(2)的变化后对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
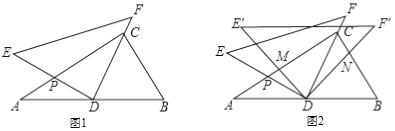
【题目】将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图1摆放,点D为AB边的中点,DE交AC于点P,DF经过点C,且BC=2.
(1)求证:△ADC∽△APD;
(2)求△APD的面积;
(3)如图2,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断![]() 的值是否随着α的变化而变化?如果不变,请求出
的值是否随着α的变化而变化?如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
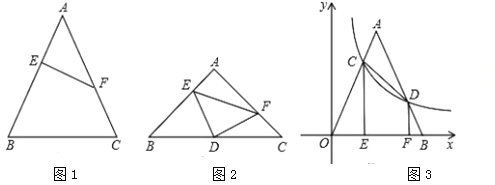
【题目】如图1,等腰![]() 中,点
中,点![]() 分别在腰
分别在腰![]() 上,连结
上,连结![]() ,若
,若![]() ,则称
,则称![]() 为该等腰三角形的逆等线.
为该等腰三角形的逆等线.
(1)如图1,![]() 是等腰
是等腰![]() 的逆等线,若
的逆等线,若![]() ,求逆等线
,求逆等线![]() 的长;
的长;
(2)如图2,若直角![]() 的直角顶点
的直角顶点![]() 恰好为等腰直角
恰好为等腰直角![]() 底边
底边![]() 上的中点,且点
上的中点,且点![]() 分别在
分别在![]() 上,求证:
上,求证:![]() 为等腰
为等腰![]() 的逆等线;
的逆等线;
(3)如图3,等腰![]() 的顶点
的顶点![]() 与原点重合,底边
与原点重合,底边![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() ,若
,若![]() 恰为
恰为![]() 的逆等线,过点
的逆等线,过点![]() 分别作
分别作![]() 轴于点
轴于点![]() 轴于点
轴于点![]() ,已知
,已知![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
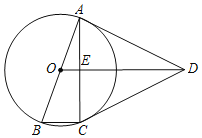
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.
(1)求证:OD∥BC;
(2)若AC=2BC,求证:DA与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
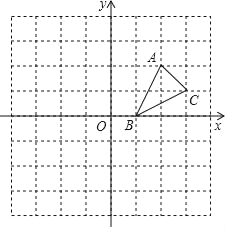
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,并写出点C2的坐标;
(3)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com