
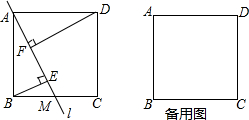
 如图,在边长为2的正方形ABCD中,点E是边AD中点,点F在边CD上,且FE⊥BE,设BD与EF交于点G,则△DEG的面积是$\frac{1}{6}$.
如图,在边长为2的正方形ABCD中,点E是边AD中点,点F在边CD上,且FE⊥BE,设BD与EF交于点G,则△DEG的面积是$\frac{1}{6}$. 分析 过点G作GM⊥AD于M,如图,先证明△ABE∽△DEF,利用相似比计算出DF=$\frac{1}{2}$,再利用正方形的性质判断△DGM为等腰直角三角形得到DM=MG,设DM=x,则MG=x,EM=1-x,然后证明△EMG∽△EDF,则利用相似比可计算出GM,再利用三角形面积公式计算S△DEG即可.
解答 解:过点G作GM⊥AD于M,如图,
∵FE⊥BE,
∴∠AEB+∠DEF=90°,
而∠AEB+∠ABE=90°,
∴∠ABE=∠DEF,
而∠A=∠EDF,
∴△ABE∽△DEF,
∴AB:DE=AE:DF,即2:1=1:DF,
∴DF=$\frac{1}{2}$,
∵四边形ABCD为正方形,
∴∠ADB=45°,
∴△DGM为等腰直角三角形,
∴DM=MG,
设DM=x,则MG=x,EM=1-x,
∵MG∥DF,
∴△EMG∽△EDF,
∴MG:DF=EM:ED,即x:$\frac{1}{2}$=(1-x):1,解得x=$\frac{1}{3}$,
∴S△DEG=$\frac{1}{2}$×1×$\frac{1}{3}$=$\frac{1}{6}$.
故答案为$\frac{1}{6}$.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.熟练运用相似比计算线段的长.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:在平面直角坐标系xOy中,一次函数y=kx+2的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.
已知:在平面直角坐标系xOy中,一次函数y=kx+2的图象与y轴交于点A,与x轴的正半轴交于点B,OA=2OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 所挂物体质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度y/cm | 18 | 20 | 22 | 24 | 26 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com