
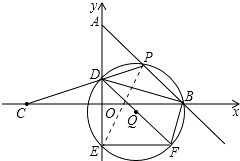
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(﹣4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.
(1)求直线AB的函数解析式;
(2)当点P在线段AB(不包括A,B两点)上时.
①求证:∠BDE=∠ADP;
②设DE=x,DF=y.请求出y关于x的函数解析式;
(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.
【答案】
(1)
解:设直线AB的函数解析式为y=kx+4,
代入(4,0)得:4k+4=0,
解得:k=﹣1,
则直线AB的函数解析式为y=﹣x+4
(2)
解:①由已知得:
OB=OC,∠BOD=∠COD=90°,
又∵OD=OD,
∴△BDO≌△CDO,
∴∠BDO=∠CDO,
∵∠CDO=∠ADP,
∴∠BDE=∠ADP,
②连结PE,
∵∠ADP是△DPE的一个外角,
∴∠ADP=∠DEP+∠DPE,
∵∠BDE是△ABD的一个外角,
∴∠BDE=∠ABD+∠OAB,
∵∠ADP=∠BDE,∠DEP=∠ABD,
∴∠DPE=∠OAB,
∵OA=OB=4,∠AOB=90°,
∴∠OAB=45°,
∴∠DPE=45°,
∴∠DFE=∠DPE=45°,
∵DF是⊙Q的直径,
∴∠DEF=90°,
∴△DEF是等腰直角三角形,
∴DF= ![]() DE,即y=
DE,即y= ![]() x
x
(3)
解:当BD:BF=2:1时,
过点F作FH⊥OB于点H,
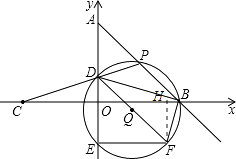
∵∠DBO+∠OBF=90°,∠OBF+∠BFH=90°,
∴∠DBO=∠BFH,
又∵∠DOB=∠BHF=90°,
∴△BOD∽△FHB,
∴ ![]() =2,
=2,
∴FH=2,OD=2BH,
∵∠FHO=∠EOH=∠OEF=90°,
∴四边形OEFH是矩形,
∴OE=FH=2,
∴EF=OH=4﹣ ![]() OD,
OD,
∵DE=EF,
∴2+OD=4﹣ ![]() OD,
OD,
解得:OD= ![]() ,
,
∴点D的坐标为(0, ![]() ),
),
∴直线CD的解析式为y= ![]() x+
x+ ![]() ,
,
由 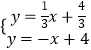 得
得 ![]() ,
,
则点P的坐标为(2,2);
当 ![]() =
= ![]() 时,
时,
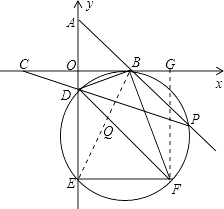
连结EB,同(2)①可得:∠ADB=∠EDP,
而∠ADB=∠DEB+∠DBE,∠EDP=∠DAP+∠DPA,
∵∠DEB=∠DPA,
∴∠DBE=∠DAP=45°,
∴△DEF是等腰直角三角形,
过点F作FG⊥OB于点G,
同理可得:△BOD∽△FGB,
∴ ![]() =
= ![]() ,
,
∴FG=8,OD= ![]() BG,
BG,
∵∠FGO=∠GOE=∠OEF=90°,
∴四边形OEFG是矩形,
∴OE=FG=8,
∴EF=OG=4+2OD,
∵DE=EF,
∴8﹣OD=4+2OD,
OD= ![]() ,
,
∴点D的坐标为(0,﹣ ![]() ),
),
直线CD的解析式为:y=﹣ ![]() x﹣
x﹣ ![]() ,
,
由  得:
得: ![]() ,
,
∴点P的坐标为(8,﹣4),
综上所述,点P的坐标为(2,2)或(8,﹣4).
【解析】(1)设直线AB的函数解析式为y=kx+4,把(4,0)代入即可;(2)①先证出△BDO≌△COD,得出∠BDO=∠CDO,再根据∠CDO=∠ADP,即可得出∠BDE=∠ADP,②先连结PE,根据∠ADP=∠DEP+∠DPE,∠BDE=∠ABD+∠OAB,∠ADP=∠BDE,∠DEP=∠ABD,得出∠DPE=∠OAB,再证出∠DFE=∠DPE=45°,最后根据∠DEF=90°,得出△DEF是等腰直角三角形,从而求出DF= ![]() DE,即y=
DE,即y= ![]() x;(3)当
x;(3)当 ![]() =2时,过点F作FH⊥OB于点H,则∠DBO=∠BFH,再证出△BOD∽△FHB,
=2时,过点F作FH⊥OB于点H,则∠DBO=∠BFH,再证出△BOD∽△FHB, ![]() =2,得出FH=2,OD=2BH,再根据∠FHO=∠EOH=∠OEF=90°,得出四边形OEFH是矩形,OE=FH=2,EF=OH=4﹣
=2,得出FH=2,OD=2BH,再根据∠FHO=∠EOH=∠OEF=90°,得出四边形OEFH是矩形,OE=FH=2,EF=OH=4﹣ ![]() OD,根据DE=EF,求出OD的长,从而得出直线CD的解析式为y=
OD,根据DE=EF,求出OD的长,从而得出直线CD的解析式为y= ![]() x+
x+ ![]() ,最后根据
,最后根据 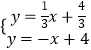 求出点P的坐标即可;当
求出点P的坐标即可;当 ![]() =
= ![]() 时,连结EB,先证出△DEF是等腰直角三角形,过点F作FG⊥OB于点G,同理可得△BOD∽△FGB,
时,连结EB,先证出△DEF是等腰直角三角形,过点F作FG⊥OB于点G,同理可得△BOD∽△FGB, ![]() =
= ![]() ,得出FG=8,OD=
,得出FG=8,OD= ![]() BG,再证出四边形OEFG是矩形,求出OD的值,再求出直线CD的解析式,最后根据
BG,再证出四边形OEFG是矩形,求出OD的值,再求出直线CD的解析式,最后根据  即可求出点P的坐标.
即可求出点P的坐标.


科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题: 
(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
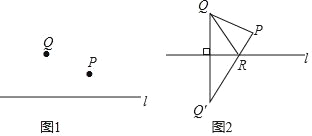
如图1,P,Q是直线l同侧两点,请你在直线l上确定一个点R,使△PQR的周长最小.
小阳的解决方法如下:
如图2,
(1)作点Q关于直线l的对称点Q;
(2)连接PQ′交直线l于点R;
(3)连接RQ,PQ.
所以点R就是使△PQR周长最小的点.
老师说:“小阳的作法正确.”
请回答:小阳的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3). 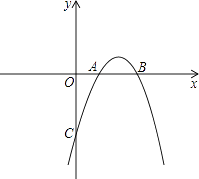
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论: ①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )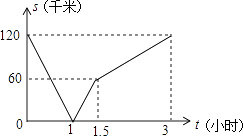
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x= ![]() . ①求该抛物线的函数解析式;
. ①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P与正方形的边碰撞的次数为 , 小球P所经过的路程为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[60°, ![]() ]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB′C′,使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com