
【题目】(问题情境)
课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.请根据小明的方法思考:

(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(初步运用)
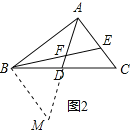
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
(灵活运用)
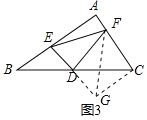
如图3,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF,试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
【答案】(1)B;(2)2<AD<10;【初步运用】BF=5;【灵活运用】BE2+CF2=EF2,理由见解析
【解析】
(1)根据全等三角形的判定定理解答;
(2)根据三角形的三边关系计算;
初步运用 延长AD到M,使AD=DM,连接BM,证明△ADC≌△MDB,根据全等三角形的性质解答;
灵活运用 延长ED到点G,使DG=ED,连结GF,GC,证明△DBE≌△DCG,得到BE=CG,根据勾股定理解答.
解:(1)在△ADC和△EDB中,
 ,
,
∴△ADC≌△EDB(SAS),
故选:B;
(2)∵△ADC≌△EDB,
∴EB=AC=8,
在△ABE中,
AB﹣BE<AE<AB+BE,
∴2<AD<10,
故答案为:2<AD<10;
【初步运用】
延长AD到M,使AD=DM,连接BM,
∵AE=EF.EF=3,
∴AC=5,
∵AD是△ABC中线,
∴CD=BD,
∵在△ADC和△MDB中,
 ,
,
∴△ADC≌△MDB,
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即BF=5;
【灵活运用】
线段BE、CF、EF之间的等量关系为:BE2+CF2=EF2.
证明:如图3,延长ED到点G,使DG=ED,连结GF,GC,
∵ED⊥DF,
∴EF=GF,
∵D是BC的中点,
∴BD=CD,
在△BDE和△CDG中,
 ,
,
∴△BDE≌△CDG(SAS),
∴BE=CG,
∵∠A=90°,
∴∠B+∠ACB=90°,
∵△BDE≌△CDG,EF=GF,
∴BE=CG,∠B=∠GCD,
∴∠GCD+∠ACB=90°,即∠GCF=90°,
∴Rt△CFG中,CF2+GC2=GF2,
∴BE2+CF2=EF2.


科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B是切点,点C是劣弧AB上的一点,若∠P=40°,则∠ACB等于( )
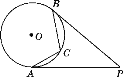
A. 80° B. 110° C. 120° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10,点E、F、G、H分别在AB、BC、CD、DA上,且满足AE∶BF∶CG∶DH=1∶2∶3∶4. 问当AE长为多少时,四边形EFGH的面积最小?并求出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上.正确的是__.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF, 则下列结论:
①△EBF≌△DFC;
②四边形AEFD为平行四边形;
③当AB=AC,∠BAC=1200时,四边形AEFD是正方形.
其中正确的结论是 .(请写出正确结论的番号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 是直线
是直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.

(1)如图1,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() .
.
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,其他条件不变,请写出
的延长线上时,其他条件不变,请写出![]() 、
、![]() 、
、![]() 三条线段之间的数量关系,并说明理由.
三条线段之间的数量关系,并说明理由.
(3)当点![]() 在线段
在线段![]() 的反向延长线上时,且点
的反向延长线上时,且点![]() 、
、![]() 分别在直线
分别在直线![]() 的两侧,其他条件不变,若
的两侧,其他条件不变,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com