
分析 (1)根据“旋转函数”的定义求出a2,b2,c2,从而得到原函数的“旋转函数”;
(2)根据“旋转函数”的定义得到-$\frac{4n}{3}$=m,-3+n=0,再解方程组求出m和n的值,然后根据乘方的意义计算;
(3)先根据抛物线与坐标轴的交点问题确定A(-1,0),B(4,0),C(0,-8),再利用关于原点对称的点的坐标特征得到A1(1,0),B1(-4,0),C1(0,8),则可利用交点式求出经过点A1,B1,C1的二次函数解析式为y=-2(x-1)(x+4)=-2x2-6x+8,再把y=2(x+1)(x-4)化为一般式,然后根据“旋转函数”的定义进行判断
解答 (1)解:∵a1=-1,b1=3,c1=-2,
∴-1+a2=0,b2=3,-2+c2=0,
∴a2=1,b2=3,c2=2,
∴函数y=-x2+3x-2的“旋转函数”为y=x2+3x+2;
(2)解:根据题意得-$\frac{4n}{3}$=m,-3+n=0,解得m=-4,n=3,
∴(m+n)2016=(-4+3)2016=1;
(3)解:当x=0时,y=2(x+1)(x-4)=-8,则C(0,-8),
当y=0时,2(x+1)(x-4)=0,解得x1=-1,x2=4,则A(-1,0),B(4,0),
∵点A、B、C关于原点的对称点分别是A1,B1,C1,
∴A1(1,0),B1(-4,0),C1(0,8),
设经过点A1,B1,C1的二次函数解析式为y=a2(x-1)(x+4),把C1(0,8)代入得a2•(-1)•4=8,解得a2=-2,
∴经过点A1,B1,C1的二次函数解析式为y=-2(x-1)(x+4)=-2x2-6x+8,
而y=2(x+1)(x-4)=2x2-6x-8,
∴a1+a2=2+(-2)=0,b1=b2=-6,c1+c2=0,
∴经过点A1、B1、C1的二次函数与函数y=2(x+1)(x-4)互为“旋转函数”.
故答案为:是.
点评 此题是二次函数综合题,熟练掌握关于原点对称的两点的坐标特征;会求二次函数图象与坐标轴的交点和待定系数法求二次函数解析式;对新定义的理解能力.解题的关键是抓住互为“旋转函数”的定义,利用函数各多项式前面的系数解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| 月龄/(月) | 1 | 2 | 3 | 4 | 5 |
| 体重/(克) | 4700 | 5400 | 6100 | 6800 | 7500 |
| A. | 7600克 | B. | 7800克 | C. | 8200克 | D. | 8500克 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
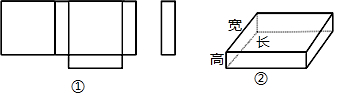
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
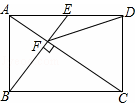 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有①②③⑤.
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有①②③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
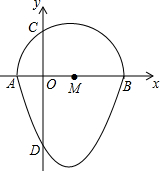 我们把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.如图,A、B、C、D分别是某蛋圆和坐标轴的交点其中抛物线的解析式为y=x2-2x-3,则“蛋圆”的弦CD的长为3+$\sqrt{3}$.
我们把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.如图,A、B、C、D分别是某蛋圆和坐标轴的交点其中抛物线的解析式为y=x2-2x-3,则“蛋圆”的弦CD的长为3+$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(-2,0),
如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(-2,0),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
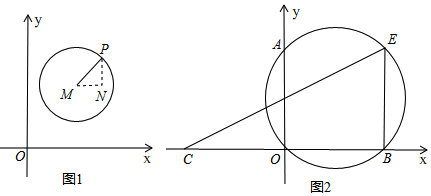
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com