
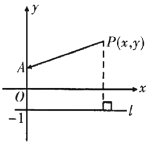
ЁОЬтФПЁПЖЈвхЃКЃЈвЛЃЉШчЙћСНИіКЏЪ§y1ЃЌy2ЃЌДцдкxШЁЭЌвЛИіжЕЃЌЪЙЕУy1ЃНy2ЃЌФЧУДГЦy1ЃЌy2ЮЊЁАКЯзїКЏЪ§ЁБЃЌГЦЖдгІxЕФжЕЮЊy1ЃЌy2ЕФЁАКЯзїЕуЁБЃЛ
ЃЈЖўЃЉШчЙћСНИіКЏЪ§ЮЊy1ЃЌy2ЮЊЁАКЯзїКЏЪ§ЁБЃЌФЧУДy1+y2ЕФзюДѓжЕГЦЮЊy1ЃЌy2ЕФЁАЙВгЎжЕЁБЃЎ
ЃЈ1ЃЉХаЖЯКЏЪ§yЃНx+2mгыyЃН![]() ЪЧЗёЮЊЁАКЯзїКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГіmЃН1ЪБЫќУЧЕФКЯзїЕуЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЪЧЗёЮЊЁАКЯзїКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГіmЃН1ЪБЫќУЧЕФКЯзїЕуЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉХаЖЯКЏЪ§yЃНx+2mгыyЃН3xЉ1ЃЈ|x|Ём2ЃЉЪЧЗёЮЊЁАКЯзїКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГіКЯзїЕуЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉвбжЊКЏЪ§yЃНx+2mгыyЃНx2ЉЃЈ2m+1ЃЉx+ЃЈm2+4mЉ3ЃЉЃЈ0ЁмxЁм5ЃЉЪЧЁАКЯзїКЏЪ§ЁБЃЌЧвгаЮЈвЛКЯзїЕуЃЎ
ЂйЧѓГіmЕФШЁжЕЗЖЮЇЃЛ
ЂкШєЫќУЧЕФЁАЙВгЎжЕЁБЮЊ24ЃЌЪдЧѓГіmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЪЧ ЁАКЯзїКЏЪ§ЁБЃЌЁАКЯзїЕуЁБЮЊxЃН2ЛђxЃНЉ4ЃЛЃЈ2ЃЉЕБЉ![]() ЁмmЁм
ЁмmЁм![]() ЪБЃЌКЏЪ§yЃНx+2mгыyЃН3xЉ1ЃЈ|x|Ём2ЃЉЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБmЃО
ЪБЃЌКЏЪ§yЃНx+2mгыyЃН3xЉ1ЃЈ|x|Ём2ЃЉЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБmЃО![]() ЛђmЃМЉ
ЛђmЃМЉ![]() ЪБЃЌКЏЪ§yЃНx+2mгыyЃН3xЉ1ЃЈ|x|Ём2ЃЉВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛЃЈ3ЃЉЂйЉ3ЁмmЃМ1Лђ2ЃМmЁм6ЃЛЂкmЃН2Љ
ЪБЃЌКЏЪ§yЃНx+2mгыyЃН3xЉ1ЃЈ|x|Ём2ЃЉВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛЃЈ3ЃЉЂйЉ3ЁмmЃМ1Лђ2ЃМmЁм6ЃЛЂкmЃН2Љ![]() ЛђmЃНЉ3+
ЛђmЃНЉ3+![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)гЩгкyЃНx+2mгыyЃН![]() ЖМОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЃЌЫљвдСНИіКЏЪ§гаЙЋЙВЕуЃЌПЩвдХаЖЯСНИіКЏЪ§ЪЧЁАКЯзїКЏЪ§ЁБЃЌдйСЊСЂx+2ЃН
ЖМОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЃЌЫљвдСНИіКЏЪ§гаЙЋЙВЕуЃЌПЩвдХаЖЯСНИіКЏЪ§ЪЧЁАКЯзїКЏЪ§ЁБЃЌдйСЊСЂx+2ЃН![]() ЃЌНтЕУxЃНЉ4ЛђxЃН2ЃЌМДПЩЧѓЁАКЯзїЕуЁБЃЛ
ЃЌНтЕУxЃНЉ4ЛђxЃН2ЃЌМДПЩЧѓЁАКЯзїЕуЁБЃЛ
(2)МйЩшЪЧЁАКЯзїКЏЪ§ЁБЃЌПЩЧѓЁАКЯзїЕуЁБЮЊxЃНm+![]() ЃЌдйгЩ|x|Ём2ЃЌПЩЕУЕБЉ
ЃЌдйгЩ|x|Ём2ЃЌПЩЕУЕБЉ![]() ЁмmЁм
ЁмmЁм![]() ЪБЃЌЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБmЃО
ЪБЃЌЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБmЃО![]() ЛђmЃМЉ
ЛђmЃМЉ![]() ЪБЃЌВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ЪБЃЌВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛ
(3)ЂйгЩвбжЊПЩЕУЃКx+2mЃНx2ЉЃЈ2m+1ЃЉx+ЃЈm2+4mЉ3ЃЉЃЌНтЕУxЃНm+3ЛђxЃНmЉ1ЃЌдйгЩвбжЊПЩЕУЕБ0Ёмm+3Ём5ЪБЃЌЉ3ЁмmЁм2ЃЌЕБ0ЁмmЉ1Ём5ЪБЃЌ1ЁмmЁм6ЃЌвђЮЊжЛгавЛИіЁАКЯзїЕуЁБдђЉ3ЁмmЃМ1Лђ2ЃМmЁм6ЃЛЂкyЃНx+2mдк0ЁмxЁм5ЕФзюДѓжЕЮЊ5+2mЃЌЕБЉ3ЁмmЃМ1ЪБЃЌКЏЪ§ЕФЖдГЦжсЉ![]() Ёмm+
Ёмm+![]() ЃМ
ЃМ![]() ЃЌДЫЪБЕБxЃН5ЪБгазюДѓжЕm2Љ6m+16ЃЛЕБ2ЃМmЁм6ЪБЃЌЖдГЦжс
ЃЌДЫЪБЕБxЃН5ЪБгазюДѓжЕm2Љ6m+16ЃЛЕБ2ЃМmЁм6ЪБЃЌЖдГЦжс![]() ЃМm+
ЃМm+![]() Ём
Ём![]() ЃЌЕБxЃН0ЪБгазюДѓжЕm2+4mЉ3ЃЛдйгЩЁАЙВгЎжЕЁБМДПЩЧѓmжЕЃЎ
ЃЌЕБxЃН0ЪБгазюДѓжЕm2+4mЉ3ЃЛдйгЩЁАЙВгЎжЕЁБМДПЩЧѓmжЕЃЎ
НтЃЛ(1)ЁпyЃНx+2mЪЧОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЕФжБЯпЃЌyЃН![]() ЪЧОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЕФЫЋЧњЯпЃЌ
ЪЧОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЕФЫЋЧњЯпЃЌ
ЁрСНКЏЪ§гаЙЋЙВЕуЃЌ
ЁрДцдкxШЁЭЌвЛИіжЕЃЌЪЙЕУy1ЃНy2ЃЌ
ЁрКЏЪ§yЃНx+2mгыyЃН![]() ЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ЕБmЃН1ЪБЃЌyЃНx+2ЃЌ
Ёрx+2ЃН![]() ЃЌНтЕУxЃНЉ4ЛђxЃН2ЃЌ
ЃЌНтЕУxЃНЉ4ЛђxЃН2ЃЌ
ЁрЁАКЯзїЕуЁБЮЊxЃН2ЛђxЃНЉ4ЃЛ
(2)МйЩшКЏЪ§yЃНx+2mгыyЃН3xЉ1ЪЧЁАКЯзїКЏЪ§ЁБЃЌ
Ёрx+2mЃН3xЉ1ЃЌ
ЁрxЃНm+![]() ЃЌ
ЃЌ
Ёп|x|Ём2ЃЌ
ЁрЉ2Ёмm+![]() Ём2ЃЌ
Ём2ЃЌ
ЁрЉ![]() ЁмmЁм
ЁмmЁм![]() ЃЌ
ЃЌ
ЁрЕБЉ![]() ЁмmЁм
ЁмmЁм![]() ЪБЃЌКЏЪ§yЃНx+2mгыyЃН3xЉ1ЃЈ|x|Ём2ЃЉЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБmЃО
ЪБЃЌКЏЪ§yЃНx+2mгыyЃН3xЉ1ЃЈ|x|Ём2ЃЉЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБmЃО![]() ЛђmЃМЉ
ЛђmЃМЉ![]() ЪБЃЌКЏЪ§yЃНx+2mгыyЃН3xЉ1ЃЈ|x|Ём2ЃЉВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ЪБЃЌКЏЪ§yЃНx+2mгыyЃН3xЉ1ЃЈ|x|Ём2ЃЉВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛ
(3)ЂйЁпКЏЪ§yЃНx+2mгыyЃНx2ЉЃЈ2m+1ЃЉx+ЃЈm2+4mЉ3ЃЉЃЈ0ЁмxЁм5ЃЉЪЧЁАКЯзїКЏЪ§ЁБЃЌ
Ёрx+2mЃНx2ЉЃЈ2m+1ЃЉx+ЃЈm2+4mЉ3ЃЉЃЌ
Ёрx2ЉЃЈ2m+2ЃЉx+ЃЈm2+2mЉ3ЃЉЃН0ЃЌ
ЁрxЃНm+3ЛђxЃНmЉ1ЃЌ
Ёп0ЁмxЁм5ЪБгаЮЈвЛКЯзїЕуЃЌ
ЕБ0Ёмm+3Ём5ЪБЃЌЉ3ЁмmЁм2ЃЌ
ЕБ0ЁмmЉ1Ём5ЪБЃЌ1ЁмmЁм6ЃЌ
ЁрЉ3ЁмmЃМ1Лђ2ЃМmЁм6ЪБЃЌТњзуЬтвтЃЛ
ЂкyЃНx+2mдк0ЁмxЁм5ЕФзюДѓжЕЮЊ5+2mЃЌ
yЃНx2ЉЃЈ2m+1ЃЉx+ЃЈm2+4mЉ3ЃЉЕФЖдГЦжсЮЊxЃНm+![]() ЃЌ
ЃЌ
ЕБЉ3ЁмmЃМ1ЪБЃЌдђЉ![]() Ёмm+
Ёмm+![]() ЃМ
ЃМ![]() ЃЌ
ЃЌ
ЕБxЃН5ЪБгазюДѓжЕЃЌзюДѓжЕЮЊm2Љ6m+16ЃЌ
Ёр5+2m+m2Љ6m+17ЃН24ЃЌ
НтЕУmЃН2+![]() ЛђmЃН2Љ
ЛђmЃН2Љ![]() ЃЌ
ЃЌ
ЁрmЃН2Љ![]() ЃЛ
ЃЛ
ЕБ2ЃМmЁм6ЪБЃЌдђ![]() ЃМm+
ЃМm+![]() Ём
Ём![]() ЃЌ
ЃЌ
ЕБxЃН0ЪБгазюДѓжЕЃЌзюДѓжЕЮЊm2+4mЉ3ЃЌ
Ёр5+2m+m2+4mЉ3ЃН24ЃЌ
НтЕУmЃНЉ3+![]() ЛђmЃНЉ3Љ
ЛђmЃНЉ3Љ![]() ЃЌ
ЃЌ
ЁрmЃНЉ3+![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃКmЃН2Љ![]() ЛђmЃНЉ3+
ЛђmЃНЉ3+![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАЂВЈТоФсАТЫЙ(Apollonius of PergaЃЌдМЙЋдЊЧА262-190Фъ)ЃЌЙХЯЃРАЪ§бЇМвЃЌгыХЗМИРяЕУЃЌАЂЛљУзЕТЦыУћЃЌЫћЕФжјзїЁЖдВзЖЧњЯпТлЁЗЪЧЙХДњЪРНчЙтЛдЕФПЦбЇГЩЙћ.
ВФСЯЃКЁЖдВзЖЧњЯпТлЁЗРяУцЖдХзЮяЯпЕФЖЈвхЃКЦНУцФквЛИіЖЏЕуЕНвЛИіЖЈЕугывЛЬѕЖЈжБЯпЕФОрРыжЎБШЕШгк1ЃЌЛђепЫЕЃКЦНУцФквЛЖЏЕуЕНвЛЖЈЕугывЛЬѕжБЯпЕФОрРыЯрЕШЕФЙьМЃОЭЪЧХзЮяЯп.
ЮЪЬтЃКвбжЊЕу![]() ЃЌ
ЃЌ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШєЕу
ЃЌШєЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыгы
ЕФОрРыгы![]() ЕФГЄЯрЕШЃЌЧыЧѓГі
ЕФГЄЯрЕШЃЌЧыЧѓГі![]() гы
гы![]() ЕФЙиЯЕЪН.
ЕФЙиЯЕЪН.
НтЃКШчЭМЃЌЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]()
Ёп![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]()
ЁпЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыгы
ЕФОрРыгы![]() ЕФГЄЯрЕШЃЌ
ЕФГЄЯрЕШЃЌ
Ёр![]() ЃЌ
ЃЌ
ЦНЗНЛЏМђЕУЃЌ![]() .
.
ШєНЋЩЯЪіЮЪЬтжа![]() ЕузјБъИФЮЊ
ЕузјБъИФЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() БфЮЊ
БфЮЊ![]() ЃЌАДееЮЪЬтНтЬтЫМТЗЃЌЪдЧѓГі
ЃЌАДееЮЪЬтНтЬтЫМТЗЃЌЪдЧѓГі![]() гы
гы![]() ЕФЙиЯЕЪНЃЌВЂдкЦНУцжБНЧзјБъЯЕжаРћгУУшЕуЗЈЛГіЦфЭМЯѓЃЌФуФмЗЂЯжЪВУДЃП
ЕФЙиЯЕЪНЃЌВЂдкЦНУцжБНЧзјБъЯЕжаРћгУУшЕуЗЈЛГіЦфЭМЯѓЃЌФуФмЗЂЯжЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГХЉПЦЫљбаОПГівЛжжаТаЭЕФЛЈЩњеЊЙћЩшБИЃЌвЛЦкбаЗЂГЩБОЮЊУПЬЈ6ЭђдЊЃЌИУеЊЙћЛњЕФЯњЪлСП![]() (ЬЈ)гыЪлМл
(ЬЈ)гыЪлМл![]() (ЭђдЊ/ЬЈ)жЎМфДцдкКЏЪ§ЙиЯЕЃК
(ЭђдЊ/ЬЈ)жЎМфДцдкКЏЪ§ЙиЯЕЃК![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЩшетжжеЊЙћЛњвЛЦкЯњЪлЕФРћШѓЮЊ![]() (ЭђдЊ)ЃЌЮЪвЛЦкЯњЪлЪБЃЌдкЧРеМЪаГЁЗнЖю(ЬсЪОЃКЯњСПОЁПЩФмДѓ)ЕФЧАЬсЯТРћШѓДяЕН32ЭђдЊЃЌДЫЪБЪлМлЮЊЖрЩйЃП
(ЭђдЊ)ЃЌЮЪвЛЦкЯњЪлЪБЃЌдкЧРеМЪаГЁЗнЖю(ЬсЪОЃКЯњСПОЁПЩФмДѓ)ЕФЧАЬсЯТРћШѓДяЕН32ЭђдЊЃЌДЫЪБЪлМлЮЊЖрЩйЃП
ЃЈ2ЃЉгЩгкЛЗБЃОжвЊЧѓИУЛњЦїБиаыдіМгГ§ГОЩшБИЃЌПЦбаЫљЭЖШыСЫ7ЭђдЊбаОПОЗбЃЌЪЙЕУЛЗБЃДяБъЧвЛњЦїЕФбаЗЂГЩБОУПЬЈНЕЕЭСЫ1ЭђдЊЃЌШєПЦбаЫљЕФЯњЪлеНТдБЃГжВЛБфЃЌЧыЮЪдкЖўЦкЯњЪлжаРћШѓДяЕН63ЭђдЊЪБЃЌИУЛњЦїЕЅЬЈЕФЪлМлЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
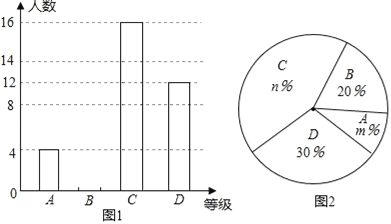
ЁОЬтФПЁП2016Фъ3дТЃЌЮвЪаФГжабЇОйааСЫЁААЎЮвжаЙњРЪЫаБШШќЁБЛюЖЏЃЌИљОнбЇЩњЕФГЩМЈЛЎЗжЮЊAЁЂBЁЂCЁЂDЫФИіЕШМЖЃЌВЂЛцжЦСЫВЛЭъећЕФСНжжЭГМЦЭМЃЎИљОнЭМжаЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЮМгРЪЫаБШШќЕФбЇЩњЙВгаЁЁ ЁЁШЫЃЌВЂАбЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЃЌm=ЁЁ ЁЁЃЌn=ЁЁ ЁЁЃЛCЕШМЖЖдгІЩШаЮгадВаФНЧЮЊЁЁ ЁЁЖШЃЛ
ЃЈ3ЃЉбЇаЃгћДгЛёAЕШМЖЕФбЇЩњжаЫцЛњбЁШЁ2ШЫЃЌВЮМгЪаОйАьЕФРЪЫаБШШќЃЌЧыРћгУСаБэЗЈЛђЪїаЮЭМЗЈЃЌЧѓЛёAЕШМЖЕФаЁУїВЮМгЪаРЪЫаБШШќЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌЭМЯѓЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпxЃН1ЃЌЯТСаНсТлЃКЂй2a+bЃН0ЃЛЂк9a+cЃО3bЃЛЂлШєЕуAЃЈЉ3ЃЌy1ЃЉЁЂЕуBЃЈЉ![]() ЃЌy2ЃЉЁЂЕуCЃЈ
ЃЌy2ЃЉЁЂЕуCЃЈ![]() ЃЌy3ЃЉдкИУКЏЪ§ЭМЯѓЩЯЃЌдђy1ЃМy3ЃМy2ЃКЂмШєЗНГЬax2+bx+cЃНЉ3ЃЈaЁй0ЃЉЕФСНИљЮЊx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђx1ЃМЉ1ЃМ3ЃМx2ЃЛЂнmЃЈam+bЃЉЉbЃМaЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
ЃЌy3ЃЉдкИУКЏЪ§ЭМЯѓЩЯЃЌдђy1ЃМy3ЃМy2ЃКЂмШєЗНГЬax2+bx+cЃНЉ3ЃЈaЁй0ЃЉЕФСНИљЮЊx1КЭx2ЃЌЧвx1ЃМx2ЃЌдђx1ЃМЉ1ЃМ3ЃМx2ЃЛЂнmЃЈam+bЃЉЉbЃМaЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉ
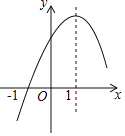
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМABЪЧАыдВЕФжБОЖЃЌЭМ1жаЃЌЕуCдкАыдВЭтЃЛЭМ2жаЃЌЕуCдкАыдВФкЃЌЧыНігУЮоПЬЖШЕФжБГпАДвЊЧѓЛЭМЃЎ
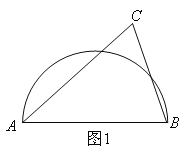
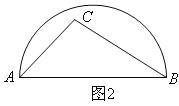
ЃЈ1ЃЉдкЭМ1жаЃЌЛГіЁїABCЕФШ§ЬѕИпЕФНЛЕуЃЛ
ЃЈ2ЃЉдкЭМ2жаЃЌЛГіЁїABCжаABБпЩЯЕФИпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
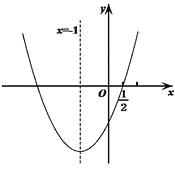
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЃЌЖдГЦжсЮЊжБЯп
ЃЌЖдГЦжсЮЊжБЯп![]() ЃЌЯТСа5ИіНсТлЃКЂй
ЃЌЯТСа5ИіНсТлЃКЂй![]() ЃЛ Ђк
ЃЛ Ђк![]() ЃЛ Ђл
ЃЛ Ђл![]() ЃЛЂм
ЃЛЂм![]() ЃЛ Ђн
ЃЛ Ђн![]() ЃЌЦфжае§ШЗЕФНсТлЮЊ________________ЃЎЃЈзЂЃКжЛЬюаДе§ШЗНсТлЕФађКХЃЉ
ЃЌЦфжае§ШЗЕФНсТлЮЊ________________ЃЎЃЈзЂЃКжЛЬюаДе§ШЗНсТлЕФађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
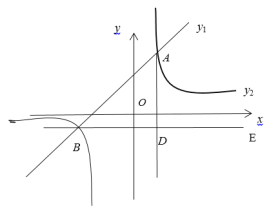
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§y1ЃНaxЃЋbЕФЭМЯёгыЗДБШР§КЏЪ§![]() ЕФЭМЯёНЛгкЕуA(2ЃЌ4)КЭB(Ѓ4ЃЌm)ЃЎ
ЕФЭМЯёНЛгкЕуA(2ЃЌ4)КЭB(Ѓ4ЃЌm)ЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЙ§ЕуBзіBE//xжсЃЌ![]() гкЕуDЃЌЕуCЪЧжБЯпBEЩЯвЛЕуЃЌШєACЃН2BCЃЌЧѓЕуCЕФзјБъЃЎ
гкЕуDЃЌЕуCЪЧжБЯпBEЩЯвЛЕуЃЌШєACЃН2BCЃЌЧѓЕуCЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЗНаЮ![]() ЁЂе§ЗНаЮ
ЁЂе§ЗНаЮ![]() ШчЭМЗХжУЃЌЕу
ШчЭМЗХжУЃЌЕу![]() дкЭЌвЛЬѕжБЯпЩЯЃЌЕу
дкЭЌвЛЬѕжБЯпЩЯЃЌЕу![]() дк
дк![]() БпЩЯЃЌ
БпЩЯЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌСЌНс
ЃЌСЌНс![]() НЛ
НЛ![]() гк
гк![]() ЃЌгаЯТСаНсТлЃКЂй
ЃЌгаЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЃЎвдЩЯНсТле§ШЗЕФИіЪ§га( )
ЃЎвдЩЯНсТле§ШЗЕФИіЪ§га( )
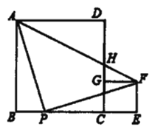
A.5ИіB.4ИіC.3ИіD.2Иі
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com