
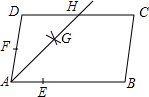
 如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )| A. | DH=BC | B. | CH=DH | C. | AG平分∠DAB | D. | AD=DH |
科目:初中数学 来源: 题型:解答题
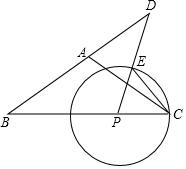 如图,在△ABC中,AB=AC=5,cosB=$\frac{4}{5}$,点P为边BC上一动点,过点P作射线PE交射线BA于点D,∠BPD=∠BAC,以点P为圆心,PC长为半径作⊙P交射线PD于点E,联结CE,设BD=x,CE=y.
如图,在△ABC中,AB=AC=5,cosB=$\frac{4}{5}$,点P为边BC上一动点,过点P作射线PE交射线BA于点D,∠BPD=∠BAC,以点P为圆心,PC长为半径作⊙P交射线PD于点E,联结CE,设BD=x,CE=y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
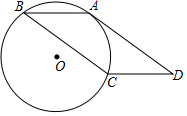 如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.
如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
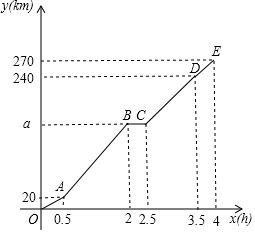 小胜一家自驾去离家(点O)270km处的某景区(点E)旅游,如图折线OABCDE表示他们离家的路程y(km)与出发的时间x(h)之间的函数图象,其中AB段的行驶速度为90km/h,BC段表示小胜一家在高速服务区下车休息.
小胜一家自驾去离家(点O)270km处的某景区(点E)旅游,如图折线OABCDE表示他们离家的路程y(km)与出发的时间x(h)之间的函数图象,其中AB段的行驶速度为90km/h,BC段表示小胜一家在高速服务区下车休息.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com