
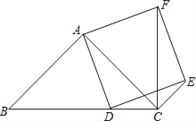
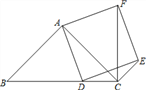
【题目】如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,以AD为边作正方形ADEF,连结CF,CE.
(1)求证:△ABD≌△ACF;
(2)如果BD=AC,求证:CD=CE.
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)根据正方形的性质得出![]() 求出
求出![]() 证出
证出![]() ≌
≌![]()
(2)根据△ABD≌△ACF,,推出![]() ,求出
,求出![]() 根据SAS推出△DAC≌△EFC即可.
根据SAS推出△DAC≌△EFC即可.
试题解析:证明:(1)∵四边形ADEF是正方形,
∴AD=AF,∠FAD=90°=∠BAC,
∴∠FAD-∠DAC=∠BAC-∠DAC,
∴∠FAC=∠BAD,
在△ABD和△ACF中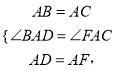
∴△ABD≌△ACF(SAS),
(2)∵△ABD≌△ACF,
∴BD=CF,
∵BD=AC,
∴AC=CF,
∴∠CAF=∠CFA,
∵四边形ADEF是正方形,
∴AD=EF,∠DAF=∠EFA=90°,
∴∠DAF-∠CAF=∠EFA-∠CFA,
∴∠DAC=∠EFC,
在△DAC和△EFC中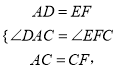
∴△DAC≌△EFC(SAS),
∴CD=CE.


科目:初中数学 来源: 题型:
【题目】如图,已知A是双曲线y= ![]() (x>0)上一点,过点A作AB∥y轴,交双曲线y=﹣
(x>0)上一点,过点A作AB∥y轴,交双曲线y=﹣ ![]() (x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为 .
(x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.

(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=10,EF=6,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y= ![]() 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.

(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
图形 | ① | ② | ③ | ④ |
顶点数(V) | ||||
边数(E) | ||||
区域数(F) |
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.

(1)填空:与∠AOE互补的角是 ;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准500、20、100、50、10的区域,顾客就可以分别获得500元、200元、100元、50元、10元的购物券一张。(转盘等分成20份)

(1)小华购物450元,他获得购物券的概率是多少?
(2)小丽购物600元,那么她获得100元以上(包括100元)券的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。
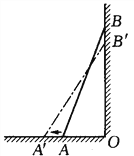
(1)这个梯子的顶端离地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com