

 AF,AG=
AF,AG= AB,求出AD=AB,推出AD=4AG,即可判断④;求出∠FAE=90°,∠AFE<90°,推出EF>AE,即可判断②;根据平行四边形性质得出AG=GF,推出S三角形AGOS三角形GOF,设AG=1,则AF=2,AB=4,BC=2,由勾股定理求出AC=2
AB,求出AD=AB,推出AD=4AG,即可判断④;求出∠FAE=90°,∠AFE<90°,推出EF>AE,即可判断②;根据平行四边形性质得出AG=GF,推出S三角形AGOS三角形GOF,设AG=1,则AF=2,AB=4,BC=2,由勾股定理求出AC=2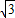 ,求出AO=OC,由勾股定理求出OE=3,得出△GOF和△EGO的面积比是1:3,即可判断⑤.
,求出AO=OC,由勾股定理求出OE=3,得出△GOF和△EGO的面积比是1:3,即可判断⑤.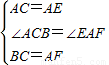 ,
,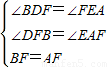 ,
, AF,AG=
AF,AG= AB,
AB,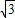 ,
,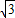 ,AO=OC=
,AO=OC=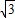 ,
,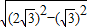 =3,
=3,

科目:初中数学 来源: 题型:
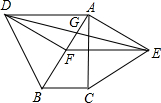 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
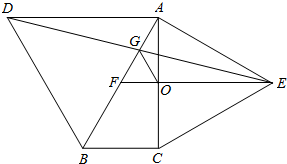 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,连接DF、EF、DE,EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,连接DF、EF、DE,EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:| A、①②③ | B、①④⑤ | C、①③⑤ | D、①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.其中正确的结论的序号是
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.其中正确的结论的序号是查看答案和解析>>
科目:初中数学 来源: 题型:
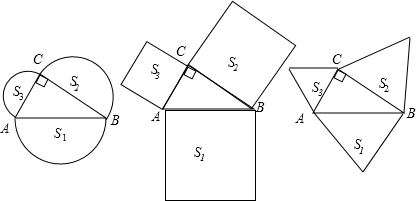
 如图,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式
如图,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com