
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
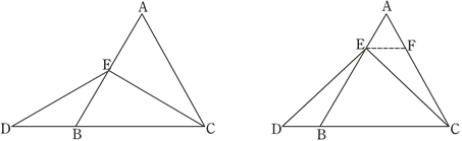
图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
【答案】(1)=;(2)=,过程见解析;(3)CD的长是1或3.
【解析】试题分析:(1)根据△ABC是等边三角形,点E为AB的中点,即可得出CE⊥AB,进而得出∠ECB=∠D=∠DEB=30°,即可得出线段AE与DB的大小关系;
(2)首先得出BE=CF,进而得出∠EDB=∠ECB,∠BED=∠FCE,进而利用△DBE≌△EFC即可得出答案;
(3)分两种情况进行讨论,①当E在线段BA的延长线上,D在线段BC的延长线上;②当E在线段AB的延长线上,D在线段CB的延长线上.
试题解析:(1)∵△ABC是等边三角形,点E为AB的中点,
∴∠ABC=60°,CE⊥AB,
∴AE=BE,
∴∠ECB=∠D=∠DEB=30°,
∴AE=DB,
故答案为:=;
(2) 在等边△ABC中,
∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠AFE=60°=∠BAC,
∴AE=AF=EF,
∴AB-AE=AC-AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED=60°,
∠ACB=∠ECB+∠FCE=60°,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∴∠BED=∠FCE,
∴△DBE≌△EFC(SAS)
∴DB=EF,
∴AE=BD,
故答案为:=;
(3)CD的长是1或3.
参考做法如下:
当E在线段BA的延长线上,D在线段BC的延长线上时,如图1所示,
过E作EF⊥BD,垂足为F点,可得∠EFB=90°,
∵EC=ED,∴F为CD的中点,即CF=DF=![]() CD,
CD,
∵△ABC为等边三角形,∴∠ABC=60°,
∴∠BEF=30°,
∵BE=AB+AE=1+2=3,
∴FB=![]() EB=
EB=![]() ,
,
∴CF=FB-BC=![]() ,
,
则CD=2CF=1;
当E在线段AB的延长线上,D在线段CB的延长线上时,如图2所示,
过E作EF⊥BD,垂足为F点,可得∠EFC=90°,
∵EC=ED,∴F为CD的中点,即CF=DF=![]() CD,
CD,
∵△ABC为等边三角形,∴∠ABC=∠EBF=60°,
∴∠BEF=30°,
∵BE=AE-AB=2-1=1,
∴FB=![]() BE=
BE=![]() ,
,
∴CF=BC+FB=![]() ,
,
则CD=2CF=3,
综上,CD的值为1或3.
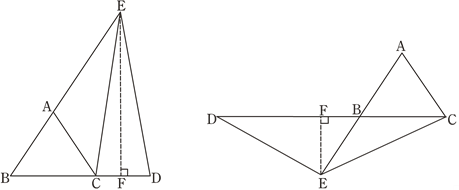
图1 图2


科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ABC=∠ACB.
(1)尺规作图:过顶点A,作△ABC的角平分线AD;(不写作法,保留作图痕迹)
(2)在AD上任取一点E,连接BE、CE.求证:BE=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
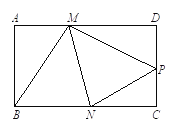
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD与点M,折痕交边BC于点N .
(1)写出图中的全等三角形. 设CP= ![]() ,AM=
,AM= ![]() ,写出
,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)试判断∠BMP是否可能等于90°. 如果可能,请求出此时CP的长;如果不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com