
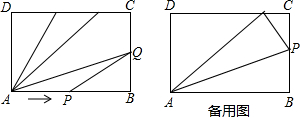
分析 (1)根据题意求出P、Q两点的速度之比,列出方程,解方程即可;
(2)根据题意分别求出点P到达点D和点Q到达点D所需的时间,计算即可;
(3)分0≤t≤2、2<t≤$\frac{10}{3}$、$\frac{10}{3}$<t≤5三个范围,根据三角形的面积公式解答即可.
解答 解:(1)∵当点P到达点B时,点Q恰好到达点C,
∴P、Q两点的速度之比为:6:4=3:2,
设点P的速度是3xcm/s,则点Q的速度是2xcm/s,
由题意得,3x-2x=1,
解得,x=1,
∴点P的速度是3cm/s,则点Q的速度是2cm/s;
(2)点P到达点D所需的时间为:(6+4+6)÷3=$\frac{16}{3}$s,
点Q到达点D所需的时间为:(6+4)÷2=5s,
∴点Q先到达点D,
则点P距离D点16-3×5=1cm,
故答案为:1;
(3)当0≤t≤2时,AP=3t,BQ=2t,
∴△APQ的面积为S=$\frac{1}{2}$×AP×BQ=3t2,
当2<t≤$\frac{10}{3}$时,BP=3t-6,CP=10-3t,CQ=2t-4,QD=10-2t,
∴△APQ的面积为S=6×4-$\frac{1}{2}$×6×(3t-6)-$\frac{1}{2}$×4×(10-2t)-$\frac{1}{2}$×(10-3t)×(2t-4)=3t2-21t+42,
当$\frac{10}{3}$<t≤5时,PQ=6-(3t-10)-[6-(2t-4)]=6-t,
∴△APQ的面积为S=$\frac{1}{2}$×PQ×AD=12-2t.
点评 本题考查的是矩形的性质、等腰三角形的性质,掌握等腰三角形的性质、灵活运用分情况讨论思想是解题的关键.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E
如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
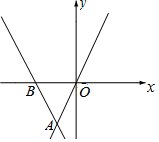 如图,直线y=kx+b经过点A(-1,m)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
如图,直线y=kx+b经过点A(-1,m)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )| A. | x<-2 | B. | -2<x<-1 | C. | -2<x<0 | D. | -1<x<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
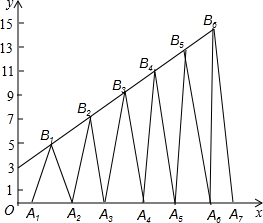 如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.
如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com