

���� ��1�����ݷǸ������������a��b��ֵ��
��2����C������A��B֮�䣬Ҳ�����ڵ�B���Ҳࣻ
��3����Ҫ�������ۣ��ټס�������������˶�����0��t��3ʱ�����ټס�������������˶�����0��t��3ʱ�������ٶȡ�ʱ�䡢����Ĺ�ϵ�г����̲����
��� �⣺��1���ߣ�3a+b��2+|b-6|=0��
��$\left\{\begin{array}{l}{3a+b=0}\\{b-6=0}\end{array}\right.$��
���a=-2��b=6��
��2�����C��ʾ������x��
�ٵ���C��A��B֮��ʱ��x-��-2��=2��6-x����
���x=$\frac{10}{3}$��
�ڵ���C��B����Ҳ�ʱ��x-��-2��=2��x-6����
���x=7��
������������C��ʾ$\frac{10}{3}$��7��
��3���ټס�������������˶�����0��t��3ʱ��
��ʱOA=2+t��OB��=6-2t��
��ɵ÷���2+t=6-2t��
���t=$\frac{4}{3}$��
�ڼ��������˶����������˶�����t��3ʱ��
��ʱOA=2+t��OB��=2t-6��
��ɵ÷���2+t=2t-6��
���t=8��
�𣺼ס�����С��ԭ��ľ������ʱ������ʱ��Ϊ$\frac{4}{3}$���8�룮
���� ���⿼����һԪһ�η��̵�Ӧ�ü������֪ʶ��ע�������δ֪����ʱ�����ǿ�������������Ȼ�������Ŀ�ĵ�����ϵ�з�����⣮


 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��A��B��C��D���ڡ�O�ϣ�CDΪ��ACE�Ľ�ƽ���ߣ�
��ͼ����֪��A��B��C��D���ڡ�O�ϣ�CDΪ��ACE�Ľ�ƽ���ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ABC=90�㣬��F��CB���ӳ�������AB=BF����F��EF��AC��AB��D����֤��DB=BC��
��ͼ����Rt��ABC�У���ABC=90�㣬��F��CB���ӳ�������AB=BF����F��EF��AC��AB��D����֤��DB=BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ʡ��������ѵ�����أ���һ��߳�Ϊ��2m+3n�������������أ���ͼ��ʾ���������������������������һ����Ϊ��2m+2n���ף���Ϊ��m+n���ij�������Ӿ�أ�ʣ�ಿ�֣�ͼ����Ӱ���֣�������Ϣ����
����ʡ��������ѵ�����أ���һ��߳�Ϊ��2m+3n�������������أ���ͼ��ʾ���������������������������һ����Ϊ��2m+2n���ף���Ϊ��m+n���ij�������Ӿ�أ�ʣ�ಿ�֣�ͼ����Ӱ���֣�������Ϣ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
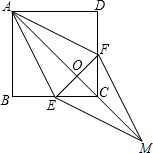 ��֪����ͼ����������ABCD�У���E��F�ֱ���BC��CD�ϣ�AE=AF������AC��EF�ڵ�O���ӳ�OC����M��ʹOM=OA������EM��FM��
��֪����ͼ����������ABCD�У���E��F�ֱ���BC��CD�ϣ�AE=AF������AC��EF�ڵ�O���ӳ�OC����M��ʹOM=OA������EM��FM���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com