
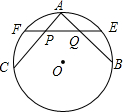
 如图所示,⊙O中AB和AC的中点分别为点E和点F,直线EF交AC于点P,交AB于点Q,那么△APQ是什么三角形?并证明你的结论.
如图所示,⊙O中AB和AC的中点分别为点E和点F,直线EF交AC于点P,交AB于点Q,那么△APQ是什么三角形?并证明你的结论. 分析 △APQ是等腰三角形.连接AE、AF,构建相似三角形--△AEQ∽△FAP,由相似三角形的对应角相等和等角的补角相等推知∠AQP=∠APQ,故△AQP为等腰三角形.
解答  解:△APQ是等腰三角形,理由如下:
解:△APQ是等腰三角形,理由如下:
如图,连接AE、AF.
∵E、F分别是弧AB、AC的中点,
∴$\widehat{AE}$=$\widehat{CE}$,$\widehat{AF}$=$\widehat{CF}$,
∴∠EAQ=∠AFP,∠AEQ=∠FAP,
∴△AEQ∽△FAP,
∴∠FPA=∠AQE,
∴∠AQP=∠APQ(等角的补角相等),
∴△AQP为等腰三角形.
点评 本题考查了圆心角、弧、弦的关系.
正确理解和使用圆心角、弧、弦三者的关系,三者关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.这源于圆的旋转不变性,即:圆绕其圆心旋转任意角度,所得图形与原图形完全重合.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平行四边形的对边平行且相等 | |
| B. | 菱形的对角线互相垂直平分 | |
| C. | 两组对边分别相等的四边形是平行四边形 | |
| D. | 对角线相等的四边形是矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com