
如图,二次函数的图象经过点D(0,![]() ),且顶点C的横坐标为4,该图象在x 轴上截得的线段AB的长为6.
),且顶点C的横坐标为4,该图象在x 轴上截得的线段AB的长为6.
⑴求二次函数的解析式;
⑵在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;
⑶在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.
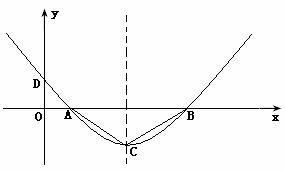
⑴设二次函数的解析式为:y=a(x-h)2+k
∵顶点C的横坐标为4,且过点(0,![]() )
)
∴y=a(x-4)2+k ![]() ………………①
………………①
又∵对称轴为直线x=4,图象在x轴上截得的线段长为6
∴A(1,0),B(7,0)
∴0=9a+k ………………②
由①②解得a=![]() ,k=
,k=![]()
∴二次函数的解析式为:y=![]() (x-4)2-
(x-4)2-![]()
⑵∵点A、B关于直线x=4对称
∴PA=PB
∴PA+PD=PB+PD≥DB
∴当点P在线段DB上时PA+PD取得最小值
∴DB与对称轴的交点即为所求点P
设直线x=4与x轴交于点M
∵PM∥OD,∴∠BPM=∠BDO,又∠PBM=∠DBO
∴△BPM∽△BDO
∴![]() ∴
∴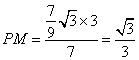
∴点P的坐标为(4,![]() )
)
⑶由⑴知点C(4,![]() ),
),
又∵AM=3,∴在Rt△AMC中,cot∠ACM=![]() ,
,
∴∠ACM=60o,∵AC=BC,∴∠ACB=120o
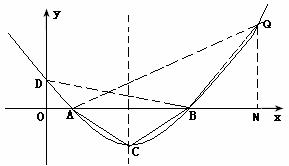
①当点Q在x轴上方时,过Q作QN⊥x轴于N
如果AB=BQ,由△ABC∽△ABQ有
BQ=6,∠ABQ=120o,则∠QBN=60o
∴QN=3![]() ,BN=3,ON=10,
,BN=3,ON=10,
此时点Q(10,![]() ),
),
如果AB=AQ,由对称性知Q(-2,![]() )
)
②当点Q在x轴下方时,△QAB就是△ACB,
此时点Q的坐标是(4,![]() ),
),
经检验,点(10,![]() )与(-2,
)与(-2,![]() )都在抛物线上
)都在抛物线上
综上所述,存在这样的点Q,使△QAB∽△ABC
点Q的坐标为(10,![]() )或(-2,
)或(-2,![]() )或(4,
)或(4,![]() ).
).


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京市华夏女子中学九年级第一学期期中考试数学卷 题型:解答题
如图是二次函数 的图象,其顶点坐标为M(1,-4).
的图象,其顶点坐标为M(1,-4).
【小题1】(1)求出图象与 轴的交点A,B的坐标;
轴的交点A,B的坐标;
【小题2】(2)在二次函数的图象上是否存在点P,使 ,若存在,求出P点的坐标;若不存在,请说明理由;
,若存在,求出P点的坐标;若不存在,请说明理由;
【小题3】(3)将二次函数的图象在 轴下方的部分沿
轴下方的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线 与此图象有两个公共点时,
与此图象有两个公共点时, 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2013年上海市中考数学模拟试卷(二)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年上海市浦东新区中考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com