
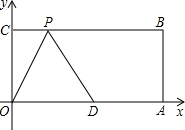
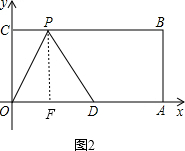
 如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为
如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为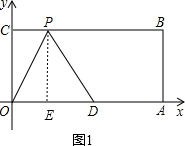


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
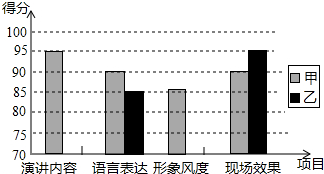 某校举办“社会主义核心价值观”知识演讲比赛,八(1)班计划从甲、乙两位同学中选出一位参加学校的决赛,已知这两位在预赛中各项成绩如表图,且甲、乙两人预赛四项成绩的平均分相同.
某校举办“社会主义核心价值观”知识演讲比赛,八(1)班计划从甲、乙两位同学中选出一位参加学校的决赛,已知这两位在预赛中各项成绩如表图,且甲、乙两人预赛四项成绩的平均分相同.| 项目 | 甲 | 乙 |
| 演讲内容 | 95 | m |
| 语言表达 | 90 | 85 |
| 形象风度 | 85 | m |
| 现场效果 | 90 | 95 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 27 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com