
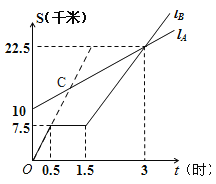
【题目】如图,![]() 、
、![]() 分别表示
分别表示![]() 步行与
步行与![]() 骑车在同一路上行驶的路程
骑车在同一路上行驶的路程![]() (千来)与时间
(千来)与时间![]() (小时)之间的关系.
(小时)之间的关系.
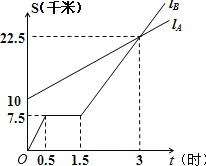
(1)![]() 出发时与
出发时与![]() 相距______千米.
相距______千米.
(2)![]() 走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)![]() 出发后______小时与
出发后______小时与![]() 相遇.
相遇.
(4)求出![]() 行走的路程
行走的路程![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(5)若![]() 的自行车不发生故障,保持出发时的速度前进,那么几小时与
的自行车不发生故障,保持出发时的速度前进,那么几小时与![]() 相遇?相遇点离
相遇?相遇点离![]() 的出发点多少千米?请同学们在图中画出这个相遇点
的出发点多少千米?请同学们在图中画出这个相遇点![]() .
.
【答案】(1)10;(2)1;(3)3;(4)![]() ;(5)
;(5)![]() 小时与
小时与![]() 相遇,相遇点离
相遇,相遇点离![]() 的出发点
的出发点![]() 千米.
千米.
【解析】
(1)从图上可看出B出发时与A相距10千米;
(2)修理的时间就是路程不变的时间是1.5-0.5=1小时;
(3)从图象看出3小时时,两个图象相交,所以3小时时相遇;
(4)S和t的函数关系是一次函数,设函数是为S=kx+t,过(0,10)和(3,22.5),从而可求出关系式;
(5)不发生故障时,B的行走的路程和时间是正比例关系,设函数式为y=kx,过(0.5,7.5)点,求出函数式,从而求出相遇的时间,从而求出路程.
(1)B出发时与A相距10千米,
故答案为:10
(2)修理自行车的时间为:1.5-05=1小时,
故答案为:1;
(3)3小时时相遇,
故答案为:3
(4)设![]() 行走的路程与时间的关系式为:
行走的路程与时间的关系式为:![]() ,
,
由图可知,函数图象经过点![]() ,
,![]() ,
,
则![]() ,解得
,解得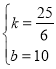 .
.
∴![]() .
.
(5)设![]() 发生故障前的函数图象表达式为:
发生故障前的函数图象表达式为:![]() ,
,
由图知,图象过点![]() ,代入
,代入![]() 中得,
中得,![]() .
.
∴![]() .
.
联立方程组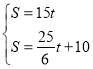 ,解得
,解得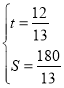 .
.
∴若![]() 的自行车不发生故障,保持出发时的速度前进,
的自行车不发生故障,保持出发时的速度前进,
则![]() 小时与
小时与![]() 相遇,相遇点离
相遇,相遇点离![]() 的出发点
的出发点![]() 千米.
千米.
在图中画出相遇点![]() :
:


科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
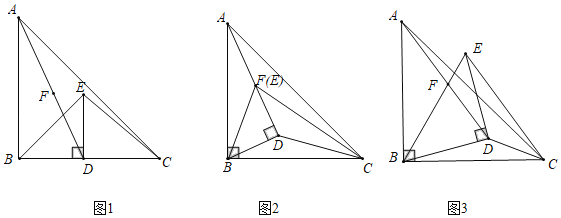
【题目】如图,在△ABC中,∠ABC=90°,AB=BC,点D为BC边上任意一点(与B、C不重合),以BD为直角边构造等腰直角三角形BDE,F为AD的中点.
(1)将△BDE绕点B旋转,当点E与F重合时,求证:∠BAE+∠BCD=45°.
(2)将△BDE绕点B旋转,当点F在BE上且AB=AD时,求证:2CD=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,国家大力提倡从纯燃油汽车向新能源汽车转型.某汽车制造企业推出了一款新型油电混合动力汽车(在行驶过程中,既可以使用汽油驱动汽年,也可以使用电力驱动汽车,汽油驱动和电力驱动不同时工作).经试验,该型汽车从甲地驶向乙地,只用汽油进行驱动,费用为56元,只用电力进行驱动,费用为20元.已知每行驶1千米,只用汽油驱动的费用比只用电力驱动的费用多0.36元.
(1)求每行驶1千米,只用汽油驱动的费用.
(2)要使从甲地到乙地所需要的燃油费用和电力费用不超过38元,则至少要用电力驱动行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠CAB=90°,AC=AB=3,△CDE中,∠CDE=90°,CD=DE=5,连接BE,取BE中点F,连接AF、DF.
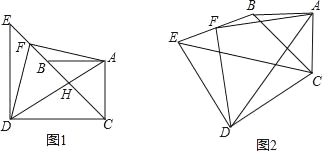
(1)如图1,若C、B、E三点共线,H为BC中点.
①直接指出AF与DF的关系 ;
②直接指出FH的长度 ;
(2)将图(1)中的△CDE绕C点逆时针旋转a(如图2,0°<α<180°),试确定AF与DF的关系,并说明理由;
(3)在(2)中,若AF=![]() ,请直接指出点F所经历的路径长.
,请直接指出点F所经历的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个车间各有工人200人,为了解这两个车间工人的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据从甲、乙两个车间各抽取20名工人进行生产技能测试,测试成绩如下:
甲:78 86 74 85 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙:93 67 88 81 72 81 94 83 77 83 80 81 64 81 73 78 82 80 70 52
整理数据按如下分数段整理、描述这两组样本数据:
50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤99 | |
甲 | 0 | _____ | 11 | ______ | 1 |
乙 | 1 | 2 | 5 | 10 | ______ |
(说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)
分析数据两组样本数据的平均数、中位数、众数如表所示:
平均数 | 中位数 | 众数 | |
甲 | _____ | 77.5 | 75 |
乙 | 78 | _____ | ______ |
得出结论可以推断_____车间工人的生产技能水平较高,理由为______.(至少从两个角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
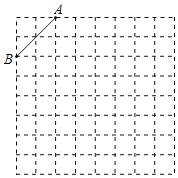
【题目】如图是8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使点A的坐标为(﹣2,4),点B的坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,连接AC,BC,使△BC成为以AB为底的等腰三角形,且腰长是无理数.
①此时点C的坐标为 ,△ABC的周长为 (结果保留根号);
②画出△ABC关于y轴对称的△A′B'C′(点A,B,C的对应点分别A',B',C′),并写出A′,B′,C′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com