



科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
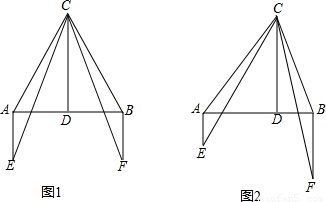
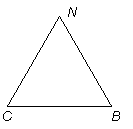
已知:如图,点![]() 为线段
为线段![]() 上一点,
上一点,![]() 、
、![]() 是等边三角形,可以说明:
是等边三角形,可以说明:![]() ≌
≌![]() ,从而得到结论:
,从而得到结论:![]() .现要求:
.现要求:
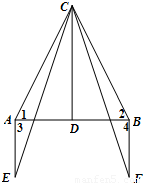
(1)将![]() 绕
绕![]() 点按逆时针方向旋转180°,使
点按逆时针方向旋转180°,使![]() 点落在
点落在![]() 上.请对照原题图在下图中画出符合要求的图形(不写作法,保留作图痕迹).
上.请对照原题图在下图中画出符合要求的图形(不写作法,保留作图痕迹).
(2)在(1)所得到的图形中,结论“![]() ”是否还成立?若成立,请给予证明;若不成立,请说明理由.
”是否还成立?若成立,请给予证明;若不成立,请说明理由.
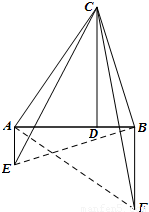
(3)在(1)所得到的图形中,设![]() 的延长线与
的延长线与![]() 相交于
相交于![]() 点,请你判断△ABD与四边形
点,请你判断△ABD与四边形![]() 的形状,并说明你的结论的正确性.
的形状,并说明你的结论的正确性.
 | |||
 | |||
查看答案和解析>>
科目:初中数学 来源:2011年江苏省南京市外国语学校中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com