
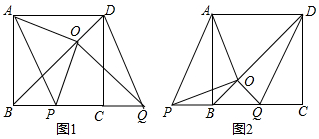
分析 (1)根据平移的性质,可得PQ,根据一组对边平行且相等的四边形是平行四边形,可得答案;
(2)根据正方形的性质,平移的性质,可得PQ与AB的关系,根据等腰直角三角形的判定与性质,可得∠PQO,根据全等三角形的判定与性质,可得AO与OP的数量关系,根据余角的性质,可得AO与OP的位置关系;
(3)根据等腰直角三角形的性质,可得OE的长,根据三角形的面积公式,可得二次函数,根据二次函数的性质,可得到答案.
解答 解:(1)四边形APQD为平行四边形;
(2)OA=OP,OA⊥OP,理由如下:
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,$\left\{\begin{array}{l}{AB=PQ}&{\;}\\{∠ABO=∠PQO}&{\;}\\{BO=QO}&{\;}\end{array}\right.$,
∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,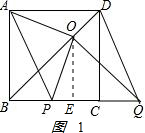
∴OA⊥OP;
(3)如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
则BQ=x+2,OE=$\frac{x+2}{2}$,
∴y=$\frac{1}{2}$×$\frac{x+2}{2}$•x,即y=$\frac{1}{4}$(x+1)2-$\frac{1}{4}$,
又∵0≤x≤2,
∴当x=2时,y有最大值为2;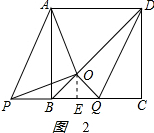
②如图2,当P点在B点左侧时,
则BQ=2-x,OE=$\frac{2-x}{2}$,
∴y=$\frac{1}{2}$×$\frac{2-x}{2}$•x,即y=-$\frac{1}{4}$(x-1)2+$\frac{1}{4}$,
又∵0≤x≤2,
∴当x=1时,y有最大值为$\frac{1}{4}$;
综上所述,当x=2时,y有最大值为2.
点评 本题是四边形综合题目,考查了二次函数的性质,利用平行四边形的判定是解题关键;利用全等三角形的判定与性质是解题关键;本题综合性强,有一定难度,利用等腰直角三角形的性质的出OE的长是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
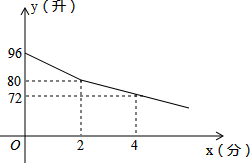 某校部分住校生,放学后到学校锅炉房打水,每人接水2L,他们同时打开两个放水龙头,后来因故障关闭一个放水龙头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(L)与接水时间x(min)的函数图象如图.
某校部分住校生,放学后到学校锅炉房打水,每人接水2L,他们同时打开两个放水龙头,后来因故障关闭一个放水龙头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(L)与接水时间x(min)的函数图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 成绩(分) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(人) | 0 | 0 | 0 | 1 | 0 | 1 | 3 | 5 | 6 | 15 | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
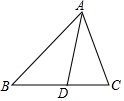 如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是$\frac{3}{5}\sqrt{10}$.
如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是$\frac{3}{5}\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
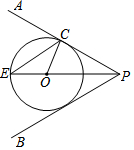 如图,∠OPA=$\frac{1}{2}$∠APB,⊙O与PA相切于点C.
如图,∠OPA=$\frac{1}{2}$∠APB,⊙O与PA相切于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
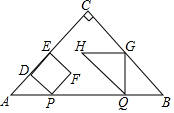 如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4cm,动点P以1cm/s的速度分别从点A、B同时出发,点P沿A→B向终点B运动,点Q沿B→A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC-CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4).
如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4cm,动点P以1cm/s的速度分别从点A、B同时出发,点P沿A→B向终点B运动,点Q沿B→A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC-CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com