Question

同一底上的两底角相等的梯形是等腰梯形吗？如果是，请给出证明（要求画出图形，写出已知、求证、证明）．如果不是，请给出反例（只需画图说明）．

Answer 1

【答案】分析：是等腰梯形．做法有多种，可以通过添加辅助线，利用等腰梯形的判定方法进行证明．
解答：解：是等腰梯形．（1分）
已知：梯形ABCD，AD∥BC且∠B=∠C（或∠A=∠D），（1分）
求证：梯形ABCD是等腰梯形．（1分）
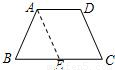
证明一：过点A作AE∥DC，交BC于E，（1分）
∵AD∥BC，AE∥DC，
∴四边形AECD是平行四边形，
∴∠AEB=∠C，AE=DC．（1分）
∵∠B=∠C，
∴∠AEB=∠B．（1分）
∴AB=AE．（1分）
∴AB=DC．
∴梯形ABCD是等腰梯形．（1分）
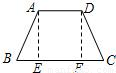
证明二：过A、D两点分别作AE⊥BC，DF⊥BC垂足为E、F，
∵AE⊥BC、DF⊥BC，
∴AE∥DF且∠AEB=∠DFC．
∵AD∥BC，
∴四边形AEFD是平行四边形．
∴AE=DF．
∵∠AEB=∠DFC，∠B=∠C，
∴△AEB≌△DFC．
∴AB=DC．
∴梯形ABCD是等腰梯形．
证明三：延长BA、CD交于E点，
∵∠B=∠C，
∴BE=CE．
∵AD∥BC，
∴∠EAD=∠B，∠EDA=∠C．
∴∠EAD=∠EDA．
∴AE=DE．
∴AB=DC．
∴梯形ABCD是等腰梯形．
点评：此题主要考查学生对等腰梯形的判定方法的掌握情况，要求学生对常用的几种判定方法熟练掌握．