
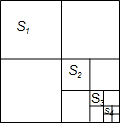
 【阅读】求值:1+2+22+23+…+22016
【阅读】求值:1+2+22+23+…+22016分析 (1)先将等式①的两边同时乘以3,再由②-①得结论;
(2)将等式①的两边同时乘以$\frac{1}{2}$,再由②-①得结论;
(3)根据题意依次求S1、S2、S3、…,得出S2016的值;
(4)将等式①的两边同时乘以$\frac{1}{4}$,再由②-①得结论;
解答 解:(1)设S=1+3+32+33+…+3100①,
将等式①的两边同时乘以3得:3S=3+32+33+…+3100+3101②,
由②-①得3S-S=3101-1,
即:S=1+3+32+33+…+3100=$\frac{{3}^{101}-1}{2}$;
(2)设S=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{100}}$①,
将等式①的两边同时乘以$\frac{1}{2}$得:$\frac{1}{2}$S=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{100}}$+$\frac{1}{{2}^{101}}$②,
由②-①得:$\frac{1}{2}$S-S=$\frac{1}{{2}^{101}}$-1,S=2-$\frac{1}{{2}^{100}}$,
即:S=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{100}}$=2-$\frac{1}{{2}^{100}}$;
(3)由题意得:S=1,S1=$\frac{1}{4}$,S2=$\frac{1}{4}$×$\frac{1}{4}$=$\frac{1}{{4}^{2}}$,S3=$\frac{1}{4}$×$\frac{1}{4}$×$\frac{1}{4}$=$\frac{1}{{4}^{3}}$,…,S2016=$\frac{1}{{4}^{2016}}$,
故答案为:$\frac{1}{{4}^{2016}}$;
(4)设A=S1+S2+S3+S4+…+S2016=1+$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+…+$\frac{1}{{4}^{2016}}$①,
将等式①的两边同时乘以$\frac{1}{4}$得:$\frac{1}{4}$A=$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+…+$\frac{1}{{4}^{2016}}$+$\frac{1}{{4}^{2017}}$②,
由②-①得:$\frac{1}{4}$A-A=$\frac{1}{{4}^{2017}}$-1,A=-$\frac{4}{3}$($\frac{1}{{4}^{2017}}$-1),
即:S1+S2+S3+S4+…+S2016=-$\frac{4}{3}$($\frac{1}{{4}^{2017}}$-1).
点评 本题是数字与图形相结合的规律题,关键是认真阅读已知材料,通过归纳与总结,得到其中的规律,并按此规律进行计算;本题还通过等分正方形的面积与数字类的规律结合在一起,进一步将数字类的规律应用到数学中来.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,折叠矩形纸片ABCD,使点B落在边AD上,折叠EF的两端分别在AB、BC上(含端点),且AB=8cm,BC=10cm,则折痕EF的最大值是8$\sqrt{2}$cm.
如图,折叠矩形纸片ABCD,使点B落在边AD上,折叠EF的两端分别在AB、BC上(含端点),且AB=8cm,BC=10cm,则折痕EF的最大值是8$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过500元 | 售价打九折 |
| 超过500元 | 售价打八折 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AE平分∠BAD交BC于点E,CE=1,∠CAE=15°,则BE等于$\frac{\sqrt{3}+1}{2}$.
如图,在矩形ABCD中,AE平分∠BAD交BC于点E,CE=1,∠CAE=15°,则BE等于$\frac{\sqrt{3}+1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com