
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
【答案】(1)(1,4);(2)(0,2);(3)k=±2.
【解析】试题分析: ![]() 根据“
根据“![]() 属派生点”计算可得;
属派生点”计算可得;
![]() 设点
设点![]() 的坐标为
的坐标为![]() 根据“
根据“![]() 属派生点”定义及
属派生点”定义及![]() ′的坐标列出关于
′的坐标列出关于![]() 的方程组,解之可得;
的方程组,解之可得;![]() 先得出点
先得出点![]() ′的坐标为
′的坐标为![]() 由线段
由线段![]() 的长度为线段
的长度为线段![]() 长度的2倍列出方程,解之可得.
长度的2倍列出方程,解之可得.
试题解析:(1)点P(1,6)的“2属派生点”P′的坐标为(1+6×2,1×2+6),即(11,4),
故答案为:(11,4);
(2)设点P的坐标为(x、y),
由题意知![]() 解得:
解得: ![]()
即点P的坐标为(0,2),
故答案为:(0,2);
(3)∵点P在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka)
∴线段PP′的长为P′到x轴距离为|ka|.
∵P在x轴正半轴,线段OP的长为a,
∴|ka|=2a,即|k|=2,
∴k=±2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(2013湖北咸宁)跳远运动员李刚对训练效果进行测试,6次跳远的成绩(单位:m)如下:7.6,7.8,7.7,7.8,8.0,7.9.这六次成绩的平均数为7.8,方差为![]() .如果李刚再跳两次,成绩分别为7.7,7.9,则李刚这8次跳远成绩的方差________.(填“变大”“不变”或“变小”)
.如果李刚再跳两次,成绩分别为7.7,7.9,则李刚这8次跳远成绩的方差________.(填“变大”“不变”或“变小”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒. 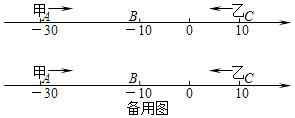
(1)甲,乙在数轴上的哪个点相遇?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A,B,C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上全班男生进行了百米测试,达标成绩为14秒,下面是第一小组8名男生的成绩记录,其中“+”表示成绩大于14秒,“﹣”表示成绩小于14秒
﹣1 | +0.8 | 0 | ﹣1.2 | ﹣0.1 | 0 | +0.5 | ﹣0.6 |
(1)求这个小组的男生达标率是多少?
(2)求这个小组8名男生的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)张师傅驾车运送草莓到某地出售,汽车出发前油箱有油50升,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量![]() (升)与行驶时间
(升)与行驶时间![]() (小时)之间的关系如图所示.
(小时)之间的关系如图所示.

请根据图象回答下列问题:
(1)汽车行驶 小时后加油,中途加油 升;
(2)求加油前油箱剩余油量![]() 与行驶时间
与行驶时间![]() 的函数关系式;
的函数关系式;
(3)已知加油前、后汽车都以70千米/小时匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否够用?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com