

分析 (1)如图1中,连接OA交BC于F.只要证明OF⊥BC即可解决问题.
(2)如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.首先证明BE=AB=AC,$\widehat{EA}$=$\widehat{CB}$,推出∠E=∠ACE,在Rt△BEM中,sin∠E=$\frac{12}{13}$,设BE=13m,则BM=12m,EM=5m,在Rt△ANC中,sin∠ACN=sin∠E=$\frac{12}{13}$,AC=EB=13m,则CN=5m,由四边形BMNA是平行四边形,推出MN=AB=EB=13m,推出CM=18m,推出tan∠BCE=$\frac{BM}{CM}$=$\frac{12m}{18m}$=$\frac{2}{3}$,可得tan∠D=$\frac{2}{3}$.
解答 (1)证明:连接OA交BC于F.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠CFO,
∵AD是⊙O的切线,
∴∠OAD=90°,
∴∠OFC=90°,
∴OF⊥BC,
∴OA平分$\widehat{BC}$,
即$\widehat{AB}$=$\widehat{AC}$.
(2)解:如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.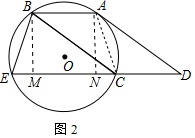
∵四边形ABCD是平行四边形,
∴∠D=∠ABC=∠BCE,
∴$\widehat{EB}$=$\widehat{CA}$,
∵$\widehat{BA}$=$\widehat{AC}$,
∴$\widehat{EB}$=$\widehat{CA}$=$\widehat{BA}$,
∴BE=AB=AC,$\widehat{EA}$=$\widehat{CB}$,
∴∠E=∠ACE,
在Rt△BEM中,sin∠E=$\frac{12}{13}$,设BE=13m,则BM=12m,EM=5m,
在Rt△ANC中,sin∠ACN=sin∠E=$\frac{12}{13}$,AC=EB=13m,则CN=5m,
∵BM=CN,BM∥CN,
∴四边形BMNA是平行四边形,
∴MN=AB=EB=13m,
∴CM=18m,
∴tan∠BCE=$\frac{BM}{CM}$=$\frac{12m}{18m}$=$\frac{2}{3}$,
∴tan∠D=$\frac{2}{3}$.
点评 本题考查切线的性质、垂径定理、平行四边形的性质、解直角三角形、锐角三角函数等知识,解题的关键是学会添加常用辅助线,学会利用参数解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )| A. | 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球 | |
| B. | 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6 | |
| C. | 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” | |
| D. | 掷一枚质地均匀的硬币,落地时结果是“正面向上” |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 西瓜质量.(单位:kg) | 3.5 | 4.8 | 5.4 | 4.9 | 4.2 | 5.0 | 4.9 | 4.8 | 5.8 | 4.8 |
| 编号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 西瓜质量.(单位:kg) | 5.0 | 4.8 | 5.2 | 4.9 | 5.1 | 5.0 | 4.8 | 6.0 | 5.7 | 5.0 |
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 西瓜质量.(单位:kg) | 4.4 | 4.9 | 4.8 | 4.1 | 5.2 | 5.1 | 5.0 | 4.5 | 4.7 | 4.9 |
| 编号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 西瓜质量.(单位:kg) | 5.4 | 5.5 | 4.0 | 5.3 | 4.8 | 5.6 | 5.2 | 5.7 | 5.0 | 5.3 |
| 优等品西瓜个数 | 平均数 | 方差 | |
| 甲种种植技术种出的西瓜质量 | 15 | 4.98 | 0.27 |
| 乙种种植技术种出的西瓜质量 | 15 | 4.97 | 0.21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
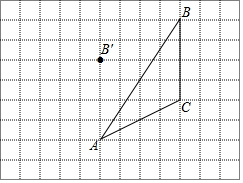 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com