
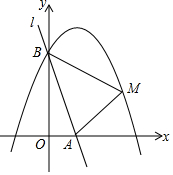
 ČēĶ¼£¬Ö±Ļßl£ŗy=-3x+3ÓėxÖį”¢yÖį·Ö±šĻą½»ÓŚA”¢BĮ½µć£¬Å×ĪļĻßy=ax2-2ax+a+4£Øa£¼0£©¾¹żµćB£®
ČēĶ¼£¬Ö±Ļßl£ŗy=-3x+3ÓėxÖį”¢yÖį·Ö±šĻą½»ÓŚA”¢BĮ½µć£¬Å×ĪļĻßy=ax2-2ax+a+4£Øa£¼0£©¾¹żµćB£®·ÖĪö £Ø1£©ĻČČ·¶Ø³öµćBµÄ×ų±ź£¬“śČėÅ×ĪļĻß½āĪöŹ½ÖŠĒó³öÅ×ĪļĻß½āĪöŹ½£»
£Ø2£©ĻČĒó³öµćAµÄ×ų±ź£¬±ķŹ¾³öMµÄ×ų±ź£¬ĄūÓĆĆ껿²ī¼“æɽØĮ¢ŗÆŹż¹ŲĻµŹ½£¬¼“æÉĒó³ö×ī“óĆ껿£»
£Ø3£©ÓÉ£Ø2£©µĆ³öµćM'µÄ×ų±ź£¬ÅŠ¶Ļ³öµ±d1+d2Č”µĆ×ī“óÖµŹ±£¬ACČ”µĆ×īŠ”Öµ£¬¼“£ŗAC”ĶB M”䏱£¬ACČ”µĆ×īŠ”Öµ£¬ÓĆ×ī“óĆ껿¼“æÉĒó³ö½įĀŪ£®
½ā“š ½ā£ŗ£Ø1£©°Ńx=0“śČėy=-3x+3µĆy=3£¬
”ąB£Ø0£¬3£©£¬
°ŃB£Ø0£¬3£©“śČėy=ax2-2ax+a+4£¬
”ą3=a+4£¬
”ąa=-1£¬
”ąy=-x2+2x+3£¬
£Ø2£©Įīy=0“śČėµĆ£ŗ0=-x2+2x+3£¬
”ąx=-1»ņ3£¬
”ąÅ×ĪļĻßÓėxÖįµÄ½»µćŗį×ų±źĪŖ-1ŗĶ3£¬
”ßMŌŚÅ×ĪļĻßÉĻ£¬ĒŅŌŚµŚŅ»ĻóĻŽÄŚ£¬
”ą0£¼m£¼3£¬
Įīy=0“śČėy=-3x+3£¬
”ąx=1£¬
”ąAµÄ×ų±źĪŖ£Ø1£¬0£©£¬
ÓÉĢāŅāÖŖ£ŗMµÄ×ų±źĪŖ£Øm£¬-m2+2m+3£©£¬
S=SĖıߊĪOAMB-S”÷AOB
=S”÷OBM+S”÷OAM-S”÷AOB
=$\frac{1}{2}$”Įm”Į3+$\frac{1}{2}$”Į1”Į£Ø-m2+2m+3£©-$\frac{1}{2}$”Į1”Į3
=-$\frac{1}{2}$m2+$\frac{5}{2}$m
=-$\frac{1}{2}$£Øm-$\frac{5}{2}$£©2+$\frac{25}{8}$
”ąµ±m=$\frac{5}{2}$Ź±£¬SČ”µĆ×ī“óÖµ$\frac{25}{8}$£»
£Ø3£©¢ŁÓÉ£Ø2£©æÉÖŖ£ŗ
µ±m=$\frac{5}{2}$Ź±£¬y=-£Ø$\frac{5}{2}$£©2+2”Į$\frac{5}{2}$+3=$\frac{7}{4}$£¬
”ąM”äµÄ×ų±źĪŖ£Ø$\frac{5}{2}$£¬$\frac{7}{4}$£©£»
¢ŚČēĶ¼£¬
¹żBµć×÷BD “¹Ö±ÓŚl”äÓŚDµć£¬¹żM”äµć×÷M”äE“¹Ö±ÓŚl”äÓŚEµć£¬
“¹Ö±ÓŚl”äÓŚDµć£¬¹żM”äµć×÷M”äE“¹Ö±ÓŚl”äÓŚEµć£¬
ŌņBD=d1£¬M”äE=d2£¬
”ßS”÷ABM”ä=$\frac{1}{2}$”ĮAC”Į£Ød1+d2£©
µ±d1+d2Č”µĆ×ī“óÖµŹ±£¬ACČ”µĆ×īŠ”Öµ£¬
”ąAC”ĶB M”䏱£¬ACČ”µĆ×īŠ”Öµ£®
”ßB£Ø0£¬3£©ŗĶM”ä£Ø$\frac{5}{2}$£¬$\frac{7}{4}$£©
”ąBM”ä=$\frac{5\sqrt{5}}{4}$£¬
”ßS”÷ABM”ä=$\frac{1}{2}$”ĮAC”ĮBM”ä=$\frac{25}{8}$£¬
”ąAC=$\sqrt{5}$£®
µćĘĄ “ĖĢāŹĒ¶ž“ĪŗÆŹż×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖ“ż¶ØĻµŹż·Ø£¬Čż½ĒŠĪĆ껿µÄ¼ĘĖć£¬¼«ÖµµÄČ·¶Ø£¬½ā£Ø1£©µÄ¹Ų¼üŹĒÓĆ“ż¶ØĻµŹż·ØĒó³öÅ×ĪļĻß½āĪöŹ½£¬½ā£Ø2£©µÄ¹Ų¼üŹĒĒó³öSÓėmµÄŗÆŹż±ķ“ļŹ½£¬½ā£Ø3£©µÄ¹Ų¼üŹĒÅŠ¶Ļ³öAC”ĶB M”䏱£¬ACČ”µĆ×īŠ”Öµ£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 3£¾|-3| | B£® | -6£¾5 | C£® | -0.2£¾0.02 | D£® | -$\frac{1}{5}$£¼-$\frac{1}{6}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
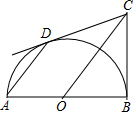 ČēĶ¼ĖłŹ¾£¬ABŹĒ°ėŌ²OµÄÖ±¾¶£¬”ĻABC=90”ć£¬µćDŹĒ°ėŌ²OÉĻŅ»¶Æµć£Ø²»ÓėµćA”¢BÖŲŗĻ£©£¬ĒŅAD”ĪCO£®
ČēĶ¼ĖłŹ¾£¬ABŹĒ°ėŌ²OµÄÖ±¾¶£¬”ĻABC=90”ć£¬µćDŹĒ°ėŌ²OÉĻŅ»¶Æµć£Ø²»ÓėµćA”¢BÖŲŗĻ£©£¬ĒŅAD”ĪCO£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 17 | B£® | 21 | C£® | 23 | D£® | 9 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
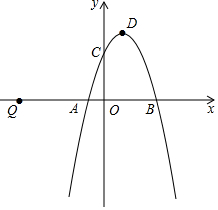 ČēĶ¼£¬¶ž“ĪŗÆŹży=mx2+£Øm2-m£©x-2m+1µÄĶ¼ĻóÓėxÖį½»ÓŚµćA”¢B£¬ÓėyÖį½»ÓŚµćC£¬¶„µćDµÄŗį×ų±źĪŖ1£®
ČēĶ¼£¬¶ž“ĪŗÆŹży=mx2+£Øm2-m£©x-2m+1µÄĶ¼ĻóÓėxÖį½»ÓŚµćA”¢B£¬ÓėyÖį½»ÓŚµćC£¬¶„µćDµÄŗį×ų±źĪŖ1£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
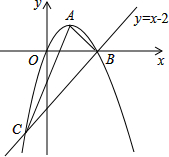 ČēĶ¼£¬ŅŃÖŖÅ×ĪļĻß¾¹żŌµćO£¬¶„µćĪŖA£Ø1£¬1£©£¬ĒŅÓėÖ±Ļßy=x-2½»ÓŚB£¬CĮ½µć£®
ČēĶ¼£¬ŅŃÖŖÅ×ĪļĻß¾¹żŌµćO£¬¶„µćĪŖA£Ø1£¬1£©£¬ĒŅÓėÖ±Ļßy=x-2½»ÓŚB£¬CĮ½µć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
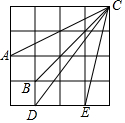 ČēĶ¼£¬Ķ¼ÖŠŹĒ16øö±ß³¤ĪŖ1µÄŠ”Õż·½ŠĪĘ“³ÉµÄ“óÕż·½ŠĪ£¬Į¬½ÓCA£¬CB£¬CD£¬CEĖÄĢõĻ߶Ī£¬ĘäÖŠ³¤¶Č¼Č²»ŹĒÕūŹżŅ²²»ŹĒ·ÖŹżµÄÓŠ3Ģõ£®
ČēĶ¼£¬Ķ¼ÖŠŹĒ16øö±ß³¤ĪŖ1µÄŠ”Õż·½ŠĪĘ“³ÉµÄ“óÕż·½ŠĪ£¬Į¬½ÓCA£¬CB£¬CD£¬CEĖÄĢõĻ߶Ī£¬ĘäÖŠ³¤¶Č¼Č²»ŹĒÕūŹżŅ²²»ŹĒ·ÖŹżµÄÓŠ3Ģõ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com