
【题目】如图①,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB=5cm,连杆BC=CD=20cm,BC,CD与AB始终在同一平面内.
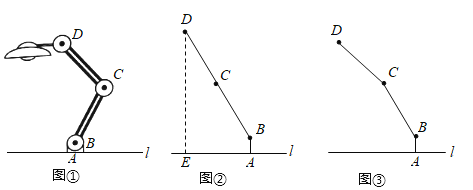
(1)如图②,转动连杆BC,CD,使∠BCD成平角,∠ABC=143°,求连杆端点D离桌面l的高度DE.
(2)将图②中的连杆CD再绕点C逆时针旋转16°,如图③,此时连杆端点D离桌面l的高度减小了 cm.
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
【答案】(1)连杆端点D离桌面l的高度DE为37cm;(2)4.
【解析】
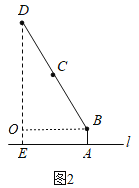
(1)如图2中,作BO⊥DE于O.解直角三角形求出OD即可解决问题.
(2)作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,求出DF,再求出DF﹣DE即可解决问题.
解:(1)作BF⊥DE于点F,则∠BFE=∠BFD=90°,
∵DE⊥l,AB⊥l,
∴∠BEA=∠BAE=90°=∠BFE.
∴四边形ABFE为矩形.
∴EF=AB=5cm,EF∥AB,
∵EF∥AB,
∴∠D+∠ABD=180°,
∵∠ABD=143°,
∴∠D=37°,
在Rt△BDF中,∵∠BFD=90°,
∴![]() =cosD=cos37°=0.8,
=cosD=cos37°=0.8,
∵DB=DC+BC=20+20=40,
∴DF=40×0.8=32,
∴DE=DF+EF=32+5=37cm,
答:连杆端点D离桌面l的高度DE为37cm;
(2)如图3,作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,
∵∠CBH=53°,∠CHB=90°,
∴∠BCH=37°,
∵∠BCD=180°﹣16°=164°,∠DCP=37°,
∴CH=BCsin53°=20×0.8=16(cm),DP=CDsin37°=20×0.6=12(cm),
∴DF=DP+PG+GF=DP+CH+AB=12+16+5=33(cm),
∴下降高度:DE﹣DF=37﹣33=4(cm).
故答案为:4.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小辉和小乐一起在学校寄宿三年了,毕业之际,他们想合理分配共同拥有的三件“财产”:一个电子词典、一台迷你唱机、一套珍藏版小说.他们本着“在尊重各自的价值偏好基础上进行等值均分”的原则,设计了分配方案,步骤如下(相应的数额如表二所示):
①每人各自定出每件物品在心中所估计的价值;
②计算每人所有物品估价总值和均分值(均分:按总人数均分各自估价总值);
③每件物品归估价较高者所有;
④计算差额(差额:每人所得物品的估价总值与均分值之差);
⑤小乐拿225元给小辉,仍“剩下”的300元每人均分.
依此方案,两人分配的结果是:小辉拿到了珍藏版小说和375元钱,小乐拿到的电子词典和迷你唱机,但要付出375元钱.
(1)甲、乙、丙三人分配A,B,C三件物品,三人的估价如表三所示,依照上述方案,请直接写出分配结果;
(2)小红和小丽分配D,E两件物品,两人的估价如表四所示(其中0<m-n<15).按照上述方案的前四步操作后,接下来,依据“在尊重各自的价值偏好基础上进行等值均分”的原则,该怎么分配较为合理?请完成表四,并写出分配结果.(说明:本题表格中的数值的单位均为“元”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克30元,规定每千克售价不低于成本,且不高于70元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 50 | 60 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某市2009年4月5日至14日每天最低气温的折线统计图.
(1)图2是该市2007年4月5日至14日每天最低气温的频数分布直方图,根据图1提供的信息,补全图2中频数分布直方图;
(2)在这10天中,最低气温的众数是____,中位数是____,方差是_____.
(3)请用扇形图表示出这十天里温度的分布情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标为(4,4),请解答下列问题:
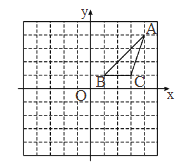
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1,B1,C1的坐标;
(2)将△ABC绕点O顺时针旋转90°,画出旋转后的△A2B2C2,并求出点B旋转到点B2所经过的路径长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,AB=5,点D是AB上的定点,点P是BC上的动点,DP绕点D逆时针旋转60°恰好落在AC上,已知BD=2,则此时DP=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
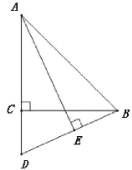
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为AC延长线上一点,连接BD,AE⊥BD于点E.
(1)记△ABC得外接圆为⊙0,
①请用文字描述圆心0的位置;
②求证:点E一定在⊙0上.
(2)将射线AE绕点A顺时针旋转45°后,所得到的射线与BD延长线交于点F,连接CF,CE.
①依题意补全图形;
②用等式表示线段AF,CE,BE的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com