
【题目】已知,△ABC(如图).
(1)利用尺规按下列要求作图(保留作图痕迹,不写作法):
①作∠BAC的平分线AD,交BC于点D;
②作AB边的垂直平分线EF,分别交AD,AB于点E,F.
(2)连接BE,若∠ABC=60°,∠C=40°,求∠AEB的度数.

科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ≈1.7,结果精确到个位).
≈1.7,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
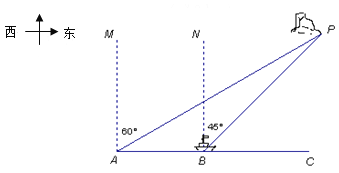
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,E是AC边上一点,EH⊥AB,垂足为H,∠1=∠2.
(1)试说明DF∥AC;
(2)若∠A=38°,∠BCD=45°,求∠3的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设某商场地下停车场有5个出入口,每天早晨7点开始对外停车且此时车位空置率为80%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满2019年元旦节期间,由于商场人数增多,早晨7点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨7点开始经过_____小时车库恰好停满.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8cm,BC=6cm.动点P、Q分别从点A、C以2cm/s的速度同时出发.动点P沿AB向终点B运动,动点Q沿CD向终点D运动,连结PQ交对角线AC于点O.设点P的运动时间为t(s).

(1)求OC的长.
(2)当四边形APQD是矩形时,直接写出t的值.
(3)当四边形APCQ是菱形时,求t的值.
(4)当△APO是等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州奥体中心是一座多功能的体育场,目前体育场内有一块长80m,宽60m的长方形空地,体育局希望将其改建成花园小广场,设计方案如图,阴影区域是面积为192平方米的绿化区(四块相同的直角三角形),空白区域为活动区,且四周出口宽度一样.

(1)体育局先对四个绿化区域进行绿化,在完成工作量的![]() 后,施工方进行了技术改进,每天的绿化面积是原计划的两倍,结果提前四天完成四个绿化区域的改造,问原计划每天绿化多少平方米?
后,施工方进行了技术改进,每天的绿化面积是原计划的两倍,结果提前四天完成四个绿化区域的改造,问原计划每天绿化多少平方米?
(2)老师提出了一个问题:你能不能求出活动区的出口宽度是多少呢?

请你根据小丽的方法求出活动区的出口宽度,并把过程写下来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com