
 如图,在三角形纸片ABC中,∠A=90°、AB=12、AC=5.折叠三角形纸片,使点A在BC边上的点E处,则AD=$\frac{10}{3}$.
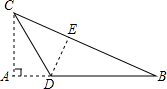
如图,在三角形纸片ABC中,∠A=90°、AB=12、AC=5.折叠三角形纸片,使点A在BC边上的点E处,则AD=$\frac{10}{3}$. 分析 先利用勾股定理求得BC=13,然后由翻折的性质可知BE=8,AD=DE,设AD=DE=x,则BD=12-x,最后再Rt△DEB中利用勾股定理求解即可.
解答 解;在Rt△ABC中,BC=$\sqrt{A{C}^{2}+A{B}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13.
由翻折的性质可知:CE=AD=5,AD=DE,∠CED=∠A=90°.
∵BE=BC-CE,
∴BE=13-5=8.
设AD=DE=x,则BD=12-x.
在Rt△DEB中,由勾股定理得:DB2=DE2+EB2,即(12-x)2=x2+82.
解得:x=$\frac{10}{3}$.
∴AD=$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用,在Rt△DEB中依据勾股定理列出关于x的方程是解题的关键.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
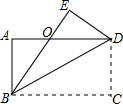 如图,将长方形纸片ABCD沿对角线BD折叠,C点对称点为E,BE交AD于点O,若∠OBD=30°,则OE与OB的数量关系为OB=2OE.
如图,将长方形纸片ABCD沿对角线BD折叠,C点对称点为E,BE交AD于点O,若∠OBD=30°,则OE与OB的数量关系为OB=2OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
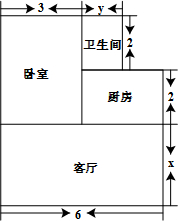 李老师家刚刚买了一套新房,他准备利用寒假铺装房子的地面,地面的结构如图所示,依据图中的数据(单位:米)解决下面的问题.
李老师家刚刚买了一套新房,他准备利用寒假铺装房子的地面,地面的结构如图所示,依据图中的数据(单位:米)解决下面的问题.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
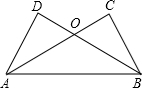 如图,AC⊥BC,AD⊥DB,下列条件中,能使△ABC≌△BAD的有①②③(把所有正确结论的序号都填在横线上)
如图,AC⊥BC,AD⊥DB,下列条件中,能使△ABC≌△BAD的有①②③(把所有正确结论的序号都填在横线上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com