
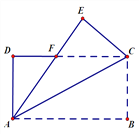
【题目】如图,在长方形ABCD中,AB=8 cm,AD=4 cm,将ΔABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点。
(1)证明:AF=CF;
(2)求ΔAFC的面积.
【答案】(1)见解析;(2)10平方厘米
【解析】试题分析:(1)根据长方形性质得出∠D=90°,AD=BC,AB=DC=8cm,根据折叠的性质得出∠D=∠E=90°,CE=BC=AD,根据全等三角形的判定得出即可;
(2)先证明△EFC≌△DFA,得出DF=EF,AF=CF,设FC=x,在RT△ADF中利用勾股定理可得出x的值,再根据三角形面积公式计算即可.
试题解析:
(1)∵四边形ABCD是长方形,
∴∠D=90°,AD=BC,AB=DC=8cm,
∵将△ABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点,
∴∠D=∠E=90°,CE=BC=AD,
在△ADF和△CEF中
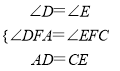 ,
,
∴△ADF≌△CEF(AAS),
∴AF=CF;
(2)∵△EFC≌△DFA(已证)
∴DF=EF,AF=CF,
设FC=x,则DF=8-x,
在RT△ADF中,DF2+AD2=AF2,即(8-x)2+16=x2,
解得:x=5,
即CF=5cm,
∴重叠部分△ACF的面积=![]() CFAD=
CFAD=![]() ×5×4=10cm2.
×5×4=10cm2.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在柯桥区2017年政府报告中提到,区政府大力推进“五水共治”、”五气合治“,五年来共投入资金24100000000元,将24100000000用科学记数法表示为( )
A. 2.41×1011 B. 2.41×1010 C. 24.1×1010 D. 0.241×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
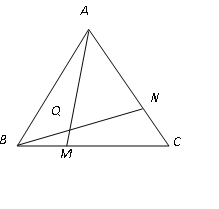
【题目】学完“等腰三角形”一章后,老师布置了一道思考题:如图,点M,N分别在正三角形![]() 的
的![]() 边上,且
边上,且![]() ,
, ![]() 交于点
交于点![]() .求证:
.求证: ![]() .
.
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“![]() ”与“
”与“![]() ”的位置交换,得到的是否仍是真命题?
”的位置交换,得到的是否仍是真命题?
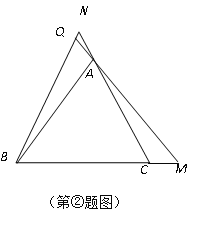
②若将题中的点![]() 分别移动到
分别移动到![]() 的延长线上,是否仍能得到
的延长线上,是否仍能得到![]() ?
?
……
请你作出判断,在下列横线上填写“是”或“否”:① ;② ;选择一个给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问 卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成 了不完整的表格和扇形统计图(如图).
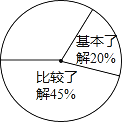
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为 人,表中m的值为 ;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
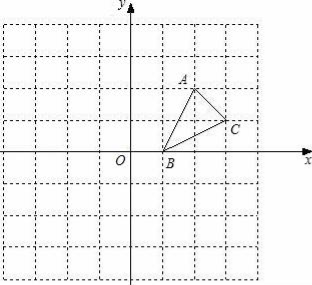
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com