
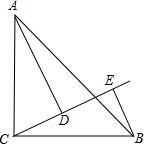
 如图:∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=5,DE=2.3,求BE的长.
如图:∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=5,DE=2.3,求BE的长. 分析 根据已知条件求得∠ACD=∠BCE,再利用角角边定理可证的△ACD≌△CBE,得出CE=AD,再根据BE=CD=CE-DE,将已知数值代入即可求得答案.
解答 解:∵∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
∴∠ACD=∠ACB-∠BCE=90°-∠BCE,∠CBE=90°-∠BCE,
∴∠ACD=∠CBE,
在△ACD与△CBE中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE(AAS).
∴CE=AD=5,
∴BE=CD=CE-DE=AD-DE=5-2.3=2.7.
答:BE的长是2.7cm.
点评 此题考查了全等三角形的判定与性质,熟练掌握等腰直角三角形的性质和全等三角形的判定与性质是本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
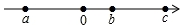 有理数a、b、c在数轴上的位置如图,
有理数a、b、c在数轴上的位置如图,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
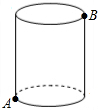 如图所示,有一圆柱,其高为12cm,它的底面周长是10cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为13 cm.
如图所示,有一圆柱,其高为12cm,它的底面周长是10cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为13 cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com