
如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
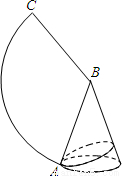
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源:2014-2015学年河北省深州市九年级上学期第三次月考数学试卷(解析版) 题型:选择题
如图,如果从半径为5cm的圆形纸片上剪去 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
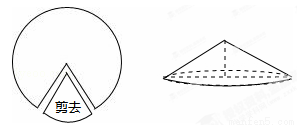
A.1cm B.3cm C.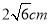 D.4cm
D.4cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期期中考试数学试卷(解析版) 题型:解答题
(12分)某商店如果将进货价为8元的商品按每件10元售出,那么每天可销售200件.现在采用提高销售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销量就减少10件.
(1)若这种商品涨价2元时,直接写出其销售量;
(2)若设这种商品的销售价为每件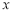 元(
元(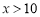 ),每天的销售利润为
),每天的销售利润为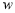 元.
元.
①要使每天获得的销售利润700元,请你帮忙确定销售价;
②问销售价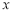 (元)定在多少元时能使每天获得的销售利润最大?并求出此时的最大利润
(元)定在多少元时能使每天获得的销售利润最大?并求出此时的最大利润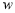 (元).
(元).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列方程是关于x的一元二次方程的是( )
A.x2 +2y+1=0
B.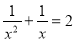
C.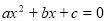
D.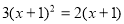
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市分校九年级上学期第三次阶段考试数学试卷(解析版) 题型:填空题
如图,在矩形ABCD中,截去一个正方形ABEF后,使剩下的矩形对开后与原矩形相似,那么原矩形中AD:AB= .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市分校九年级上学期第三次阶段考试数学试卷(解析版) 题型:选择题
在四边形ABCD中,AC平分∠BAD,且∠ACD=∠B。则下列结论中正确的是( )
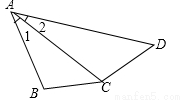
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福安市小片区九年级上学期半期考试数学试卷(解析版) 题型:填空题
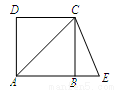
如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期中检测数学试卷(解析版) 题型:解答题
已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
(1)如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;

小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.
请你借鉴小明的方法写出AM的长,并写出推理过程.
(2)若△ABC为等腰直角三角形,∠BAC= ,
,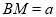 ,
,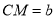 (其中
(其中 ),直接写出AM的长(用含有a,b的代数式表示).
),直接写出AM的长(用含有a,b的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com