
【题目】已知二次函数y=ax2﹣4ax+1
(1)写出二次函数图象的对称轴:_____;
(2)如图,设该函数图象交x轴于点A、B(B在A的右侧),交y轴于点C.直线y=kx+b经过点B、C.
①如果k=﹣![]() ,求a的值
,求a的值
②设点P在抛物线对称轴上,PC+PB的最小值为![]() ,求点P的坐标.
,求点P的坐标.

【答案】(1)直线x=2;(2)① a=3;②![]() .
.
【解析】分析:
(1)由二次函数![]() 的对称轴为直线
的对称轴为直线![]() 进行解答即可;
进行解答即可;
(2)①在![]() 由x=0可得y=1,由此可得点C的坐标,从而可得b的值,结合k=
由x=0可得y=1,由此可得点C的坐标,从而可得b的值,结合k=![]() 可得直线BC的解析式为
可得直线BC的解析式为![]() ,由此即可解得点B的坐标,将所得点B的坐标代入
,由此即可解得点B的坐标,将所得点B的坐标代入![]() 中即可解得此时a的值;②由图可知,当点P为BC与抛物线对称轴的交点时,PB+PC最小,此时BC=
中即可解得此时a的值;②由图可知,当点P为BC与抛物线对称轴的交点时,PB+PC最小,此时BC=![]() ,结合OC=1,由勾股定理即可解得此时OB的长,从而可得此时点B的坐标,将点B的坐标代入
,结合OC=1,由勾股定理即可解得此时OB的长,从而可得此时点B的坐标,将点B的坐标代入![]() 中即可求得此时BC的解析式,由此即可求得此时点P的坐标了.
中即可求得此时BC的解析式,由此即可求得此时点P的坐标了.
详解:
(1)二次函数y=ax2﹣4ax+1的图象的对称轴为直线![]() .
.
故答案为:直线x=2.
(2)①当x=0时,y=1,
∴点C的坐标为(0,1).
将(0,1)代入y=kx+b,得:b=1.
∵k=![]() ,
,
∴![]() ,
,
当y=0时,有![]() ,
,
解得:x=3,
∴点B的坐标为(3,0).
将B(3,0)代入y=ax2﹣4ax+1,得:
9a﹣12a+1=0,
解得:a=3;
②当PC+PB取最小值时,点P是直线BC与直线x=2的交点,且PC+PB的最小值=BC=![]() .
.
∵OC=1,
∴在Rt△OBC中,OB=![]() ,
,
∴此时点B的坐标为![]() ,
,
将点B的坐标代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∴此时直线BC的解析式为:![]() ,
,
∵当![]() 时,
时,![]() ,
,
∴点P的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“诗词大赛”预赛.参赛选手的成绩如下(单位:分)
九(1)班:88,91,92,93,93,93,94,98,99,100
九(2)班:89,93,93,93,95,96,96,96,98,99.
(1)九(2)班的平均分是 分;九(1)班的众数是 分;
(2)若从两个班成绩最高的5位同学中选2人参加市级比赛,则这两个人来自不同班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
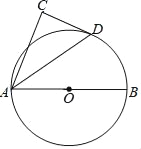
【题目】如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB
(1)求证:DC是⊙O的切线;
(2)若AB=9,AD=6,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节吃粽子是中华民族的传统习惯.农历五月初五早晨,小王的妈妈用不透明袋子装着一些粽子(粽子除食材不同外,其他一切相同),其中糯米粽两个,还有一些薯粉粽,现小王从中任意拿出一个是糯米粽的概率为![]() .
.
(1)求袋子中薯粉粽的个数;
(2)小王第一次任意拿出一个粽子(不放回),第二次再拿出一个粽子,请你用树形图或列表法,求小王两次拿到的都是薯粉粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴ 探究发现
① ![]() _________;
_________;
② ![]() _________;
_________;
③ ![]() _________;
_________;
④ _________________;
… …
⑵ 规律提炼
写出第n个等式(用含有字母![]() 的式子表示).
的式子表示).
⑶ 问题解决
① ![]() _______;
_______;
② 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个游戏的中奖概率是![]() ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖
B. 为了解全国中学生的心理健康情况,应该采用普查的方式
C. 一组数据6,8,7,8,8,9,10的众数和中位数都是8
D. 若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合例
-2.5,-0.151515…,0,8,![]() ,
,![]() ,
,![]() ,-0.5252252225…(每两个5之间依次增加1个2)
,-0.5252252225…(每两个5之间依次增加1个2)
正数:{___________________________________________________…};
负分数:{___________________________________________________…};
整数:{___________________________________________________…}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com