Question

如图,在直角梯形ABCD中，以Ｂ点为原点建立直角坐标系，AB∥CD,AD⊥DC,　AB=BC,　且AE⊥BC.

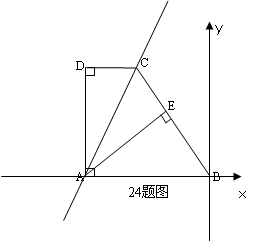
⑴ 求证：AD=AE；

⑵ 若AD=8，DC=4，AB=10，求直线AC的解析式.

⑶在（2）中的条件下，在直线AC上是否存在P点，使得△PAD的面积等于△ABE的面积？若存在，请求出P的坐标；若不存在，请说明理由。

Answer 1

（1）证明△ADC≌△AEC得AD =AE （2）直线AC的解析式为

（3）存在P点，使得△PAD的面积等于△ABE的面积

【解析】

试题分析：（1）∵AB∥CD∴∠ACD=∠BAC

∵AB=BC

∴∠ACB =∠BAC

∴∠ACD =∠ACB

∵AD⊥DC ，AE⊥BC

∴∠D =∠AEC=90⁰

∵AC=AC 　　　　　　　

∴△ADC≌△AEC　　　 　

∴AD =AE　　　　　　　　

（2）若AD=8，DC=4，AB=10，根据图形C点的纵坐标等于AD，横坐标等于AB-CD的相反数，因为AB-CD=10-4=6，所以点C的坐标为（-6,8），观察图形得点A的坐标为（-10，0），设直线AC的解析式为，则，解得，所以直线AC的解析式为

（3）存在

易求得=24，设△PAD的边AD上的高为h，则由得，得h=6，

所以Ｐ的横坐标为－4或－16,代人得纵坐标为12或-12

所以P的坐标为（-4,12）或（-16，-12）

考点：全等三角形、一次函数

点评：本题考查全等三角形、一次函数，解答本题需要掌握全等三角形的判定方法、熟悉一次函数，掌握待定系数法，会用待定系数法求函数的解析式