【题目】如图，矩形
中，
，以
为直径作
.
（1）证明:
是的切线；
（2）若
，连接
，求阴影部分的面积.(结果保留
)
【答案】（1）见解析；（2）
【解析】
（1）过O点作OE⊥CD于E点，证四边形OEBC为正方形，可得OE为半径，问题即可得证.
（2）连接BE，S阴影=S△BED+（S扇形OBE-S△BOE），代入数值求解即可.
（1）过O点作OE⊥CD于E点，则∠OEC=90°
∵四边形ABCD为矩形
∴∠ABC=∠BCE=90°
∴四边形OECB为矩形
又AB=2BC，AB=2OB
∴OB=BC
∴四边形OBCE为正方形
∴OE=OB
又OE⊥CD
故CD为
O的切线.
（2）连接BE,
由（1）可得：四边形OBCE为正方形
∴OB=OE=EC=OB=3，DC=AB=6，DE=3
∴S阴影=S△BED+（S扇形OBE-S△BOE）=
A加金题 系列答案
全优测试卷系列答案科目：初中数学 来源： 题型：
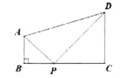
【题目】如图,四边形ABCD中,AB∥CD,∠B=90°,AB=1,CD=2,BC=3,点P为BC边上一动点,若△PAB与△PCD是相似三角形,则BP的长为 _____________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知平行四边形ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=50°，则∠DA′E′的度数为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
与双曲线
相交于
，
两点，点坐标为(－3，2)，点坐标为(n，－3).
(1)求一次函数和反比例函数的表达式；
(2)如果点
是
轴上一点，且
的面积是5，求点的坐标.
(3)利用函数图象直接写出关于x的不等式
的解集．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：小胖同学遇到这样一个问题，如图1，在△ABC中，∠ABC＝45°，AB＝2
，AD＝AE，∠DAE＝90°，CE＝
，求CD的长；
小胖经过思考后，在CD上取点F使得∠DEF＝∠ADB（如图2），进而得到∠EFD＝45°，试图构建“一线三等角”图形解决问题，于是他继续分析，又意外发现△CEF∽△CDE．
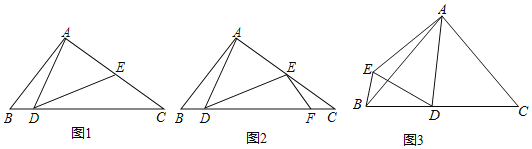
（1）请按照小胖的思路完成这个题目的解答过程．
（2）参考小胖的解题思路解决下面的问题：
如图3，在△ABC中，∠ACB＝∠DAC＝∠ABC，AD＝AE，
∠EAD+∠EBD＝90°，求BE：ED．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，E是边CD上一点（点E不与点C，D重合），连接BE．取BE的中点M，过点M作FG⊥BE交BC于点F，交AD于点G．
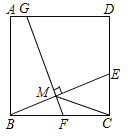
（1）求证：BE＝FG．
（2）连接CM，若CM＝1，试求FG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
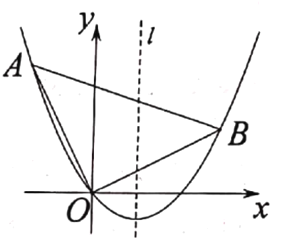
【题目】在平面直角坐标系中，△AOB的位置如图所示，∠AOB=90°，AO=BO，点A的坐标为(-1， 2) .抛物线y = ax2 + bx (a≠0)恰好经过A， B两点.
(1)直接写出点B坐标 .
(2)求该抛物线的函数表达式.
(3)设A关于抛物线的对称轴l的对称点为A'，求△AA' B的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
