
 (1)用列表,描点的方法在同意直角坐标系中画出函数y=x+2和y=x2的图象
(1)用列表,描点的方法在同意直角坐标系中画出函数y=x+2和y=x2的图象科目:初中数学 来源: 题型:填空题
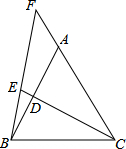 如图,△ABC为等边三角形,D为AB上一点,点E为CD延长线上一点,CE=CB,连接BE并延长交CA的延长线于点F,若AD=3,CF=7,则CD=4.
如图,△ABC为等边三角形,D为AB上一点,点E为CD延长线上一点,CE=CB,连接BE并延长交CA的延长线于点F,若AD=3,CF=7,则CD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
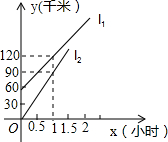 已知A,B地相距225千米,甲,乙两车都从A地出发,沿同一条高速公路前往B地,甲比乙早出发1小时,如图所示的l1,l2分别表示甲乙两车相对于出发地A的距离y(千米)与乙车行驶时间x(小时)之间的关系.根据图象提供的信息,解答下列问题:
已知A,B地相距225千米,甲,乙两车都从A地出发,沿同一条高速公路前往B地,甲比乙早出发1小时,如图所示的l1,l2分别表示甲乙两车相对于出发地A的距离y(千米)与乙车行驶时间x(小时)之间的关系.根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $±\sqrt{2}$ | B. | $±\sqrt{3}$ | C. | ±2 | D. | ±1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
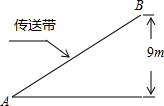 如图,传送带和地面所成的斜坡的坡度为1:$\sqrt{3}$,它把物体从地面送到离地面9米高的地方,则物体从A到B所经过的路程为18米.
如图,传送带和地面所成的斜坡的坡度为1:$\sqrt{3}$,它把物体从地面送到离地面9米高的地方,则物体从A到B所经过的路程为18米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com