
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧 ![]() (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( ) 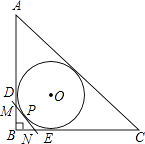
A.r
B.![]() ?r
?r
C.2r
D.![]() ?r
?r
【答案】C
【解析】解:连接OD、OE, ∵⊙O是Rt△ABC的内切圆,
∴OD⊥AB,OE⊥BC,
∵∠ABC=90°,
∴∠ODB=∠DBE=∠OEB=90°,
∴四边形ODBE是矩形,
∵OD=OE,
∴矩形ODBE是正方形,
∴BD=BE=OD=OE=r,
∵⊙O切AB于D,切BC于E,切MN于P,NP与NE是从一点出发的圆的两条切线,
∴MP=DM,NP=NE,
∴Rt△MBN的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r,
故选C.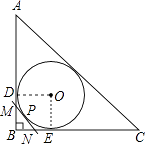
【考点精析】根据题目的已知条件,利用切线长定理和矩形的判定方法的相关知识可以得到问题的答案,需要掌握从圆外一点引圆的两条切线,它们的切线长相等圆心和这一点的连线平分两条切线的夹角;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连接CF. 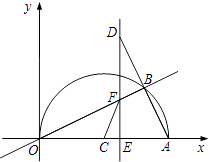
(1)当∠AOB=30°时,求弧AB的长度;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似?若存在,请求出此时点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°. 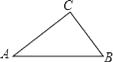
(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法) ①作AC的垂直平分线,交AB于点O,交AC于点D;
②以O为圆心,OA为半径作圆,交OD的延长线于点E.
(2)在(1)所作的图形中,解答下列问题. 点B与⊙O的位置关系是;(直接写出答案)
(3)若DE=2,AC=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,直线y= ![]() x+6与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
x+6与x轴、y轴分别交于点A、C两点,点B的横坐标为2. 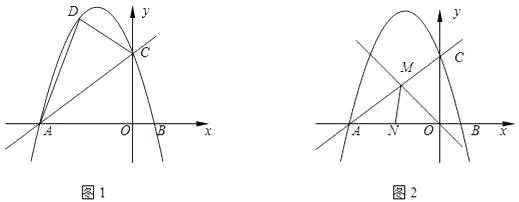
(1)求A、C两点的坐标和抛物线的函数关系式;
(2)点D是直线AC上方抛物线上任意一点,P为线段AC上一点,且S△PCD=2S△PAD , 求点P的坐标;
(3)如图2,另有一条直线y=﹣x与直线AC交于点M,N为线段OA上一点,∠AMN=∠AOM.点Q为x轴负半轴上一点,且点Q到直线MN和直线MO的距离相等,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 三对数值中,________是方程x+y=3的解,________是方程3x+2y=5的解,________是方程组
三对数值中,________是方程x+y=3的解,________是方程3x+2y=5的解,________是方程组![]() 的解.(填序号)
的解.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB:BC=3:4,AC=5,点P从点A出发,以每秒1个单位的速度,沿△ABC边A→B→C→A的方向运动,运动时间为t秒.
(1)求AB与BC的长;
(2)在点P的运动过程中,是否存在这样的点P,使△CDP为等腰三角形?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,点C、D在线段AB上,D是线段AB的中点,AC=![]() AD ,CD=4 ,求线段AB的长.
AD ,CD=4 ,求线段AB的长.
![]()
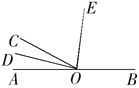
(2)如图,点O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线,若∠AOD=14°,求∠DOE、∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部B处的仰角为45°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC(结果精确到0.1米)(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)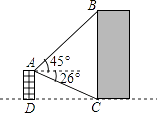
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com