
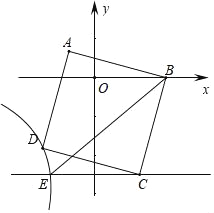
【题目】如图1,抛物线y=ax2+bx+c的图象与x轴交于A(﹣3,0)、B(1,0)两点,与y轴交于点C,且OC=OA.
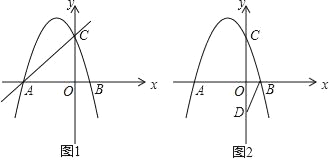
(1)求抛物线解析式;
(2)过直线AC上方的抛物线上一点M作y轴的平行线,与直线AC交于点N.已知M点的横坐标为m,试用含m的式子表示MN的长及△ACM的面积S,并求当MN的长最大时S的值;
(3)如图2,D(0,﹣2),连接BD,将△OBD绕平面内的某点(记为P)逆时针旋转180°得到△O′B′D′,O、B、D的对应点分别为O′、B′、D′.若点B′、D′两点恰好落在抛物线上,求旋转中心点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)MN=﹣m2﹣3m(﹣3<m<0),S△ACM=![]() ,m=﹣
,m=﹣![]() 时,MN最大,此时S=
时,MN最大,此时S=![]() ;(3)P(-
;(3)P(-![]() ,
,![]() ).
).
【解析】
(1)先求出点A坐标,再运用待定系数法求解即可;
(2)先求出直线AC的解析式,待定点M,N的坐标,用m表示线段MN的长度,运用二次函数分析其最值即可;
(3)根据中心对称的性质,明确B′D′与BD平行且相等,待定点B′、D′的坐标,代入抛物线解析式求解即可得出B′、D′的坐标,而后运用中点公式求出中心的坐标即可;
解:(1)由A(﹣3,0),且OC=OA可得
A(﹣3,0)
设抛物线解析式为y=a(x+3)(x﹣1),
将C(0,3)代入解析式得,﹣3a=3,解得a=﹣1,
∴抛物线解析式为y=﹣x2﹣2x+3.
(2)如图1,
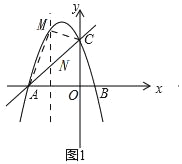
设直线AC解析式为y=kx+d
∵A(﹣3,0),C(0,3),
∴![]() ,
,
解得![]() ,
,
∴直线AC解析式为y=x+3,
设M(m,﹣m2﹣2m+3),则N(m,m+3),则MN=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m(﹣3<m<0),
S△ACM=S△AMN+S△CMN=![]() MN×3=
MN×3=![]() ,
,
MN=﹣m2﹣3m=﹣![]() +
+![]() ,
,
∵a=﹣1<0,﹣3<m=﹣1.5<0,
∴m=﹣![]() 时,MN最大,此时S=
时,MN最大,此时S=![]() ;
;
(3)如图2中,旋转180°后,对应线段互相平行且相等,则BD与B′D′互相平行且相等.
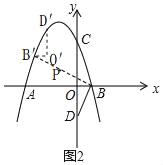
∵O′B′=OB=1,O′D′=OD=2,
设B′(t,﹣t2﹣2t+3),则D′(t+1,﹣t2﹣2t+3+2)
∵D′在抛物线上,则﹣(t+1)2﹣2(t+1)+3=﹣t2﹣2t+3+2,
解得,t=-![]() ,则B′的坐标为(-
,则B′的坐标为(-![]() ,
,![]() ),
),
P是点B(1,0)和点B′(-![]() ,
,![]() ),的对称中心,
),的对称中心,
![]() ,
,![]() ,
,
∴P(-![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】我市智慧阅读活动正如火如茶地进行.某班学习委员为了解11月份全班同学课外阅读的情况,调查了全班同学11月份读书的册数,并根据调查结果绘制了如下不完整的条形统计图和扇形统计图:
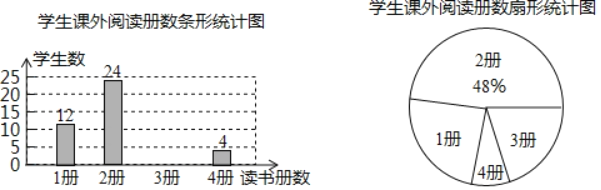
(1)扇形统计图中“3册”部分所对应的圆心角的度数是 ,并把条形统计图补充完整;
(2)该班的学习委员11月份的读书册数为4册,若该班的班主任从11月份读书4册的学生中随机抽取两名同学参加学校举行的知识竞赛,请用列表法或画树状图求恰好有一名同学是学习委员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论错误的是( )
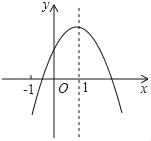
A. 4a+2b+c>0B. abc<0C. b<a﹣cD. 3b>2c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
有n个环环相扣的圆环形成一串线型链条,当只断开其中的k(k<n)个环,要求第一次取走一个环,以后每次都只能比前一次多得一个环,则最多能得到的环数n是多少呢?
问题探究:
为了找出n与k之间的关系,我们运用一般问题特殊化的方法,从特殊到一般,归纳出解决问题的方法.
探究一:k=1,即断开链条其中的1个环,最多能得到几个环呢?
当n=1,2,3时,断开任何一个环,都能满足要求,分次取走;
当n=4时,断开第二个环,如图①,第一次取走1环;第二次退回1环换取2环,得2个环;第三次再取回1环,得3个环;第四次再取另1环,得4个环,按要求分4次取走.
当n=5,6,7时,如图②,图③,图④方式断开,可以用类似上面的方法,按要求分5,6,7次取走.
当n=8时,如图⑤,无论断开哪个环,都不可能按要求分次取走.
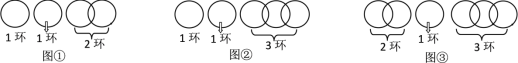
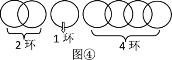
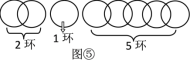
所以,当断开1个环时,从得到更多环数的角度考虑,把链条分成3部分,分别是1环、2环和4环,最多能得到7个环.
即当k=1时,最多能得到的环数n=1+2+4=1+2×3=1+2×(22-1)=7.
探究二:k=2,即断开链条其中的2个环,最多能得到几个环呢?
从得到更多环数的角度考虑,按图⑥方式断开,把链条分成5部分,按照类似探究一的方法,按要求分1,2,…23次取走.
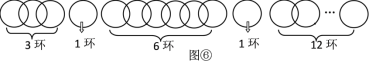
所以,当断开2个环时,把链条分成5部分,分别是1环、1环、3环、6环、12环,最多能得到23个环.
即当k=2时,最多能得到的环数n=1+1+3+6+12=2+3×7=2+3×(23-1)=23.
探究三:k=3,即断开链条其中的3个环,最多能得到几个环呢?
从得到更多环数的角度考虑,按图⑦方式断开,把链条分成7部分,按照类似前面探究的方法,按要求分1,2,…63次取走.
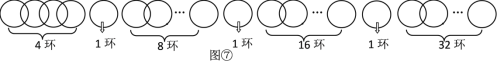
所以,当断开3个环时,从得到更多环数的角度考虑,把链条分成7部分,分别是1环、1环、1环、4环、8环、16环、32环,最多能得到63个环.
即当k=3时,最多能得到的环数n=1+1+1+4+8+16+32=3+4×15=3+4×(24-1)=63.
探究四:k=4,即断开链条其中的4个环,最多能得到几个环呢?
按照类似前面探究的方法,当断开4个环时,从得到更多环数的角度考虑,把链条分成 部分,分别为 ,最多能得到的环数n= .请画出如图⑥的示意图.
模型建立:
有n个环环相扣的圆环形成一串线型链条,断开其中的k(k<n)个环,从得到更多环数的角度考虑,把链条分成 部分,
分别是:1、1、1……1、k+1、 、……、 ,最多能得到的环数n = .
实际应用:
一天一位财主对雇工说:“你给我做两年的工,我每天付给你一个银环.不过,我用一串环环相扣的线型银链付你工钱,但你最多只能断开银链中的6个环.如果你无法做到每天取走一个环,那么你就得不到这两年的工钱,如果银链还有剩余,全部归你!你愿意吗?”
聪明的你是否可以运用本题的方法通过计算帮助雇工解决这个难题,雇工最多能得到总环数为多少环的银链?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x二次函数y=x2﹣(2k+1)x+(k2+5k+9)与x轴有交点.
(1)求k的取值范围;
(2)若x1,x2是关于x的方程x2﹣(2k+1)x+(k2+5k+9)=0的两个实数根,且x12+x22=39,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
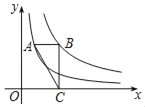
【题目】如图,点A在反比例函数y=![]() (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=![]() (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
(x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=![]() 上,过点C作CE∥x轴交双曲线于点E,连接BE,则△BCE的面积为( )
上,过点C作CE∥x轴交双曲线于点E,连接BE,则△BCE的面积为( )
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( ).

A.22 B.24 C.10![]() D.12
D.12![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com