练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    有条小河l，点A，B表示在河两岸的两个村庄，现在要建造一座小桥，请你找出造桥的位置，使得到A，B两村的路程最短，并说明理由．

    答案：
    解析：

    　　解：如图：过点A，B作线段AB，与直线l的交点P为所求的点，因为两点之间，线段最短．


    提示：

    由“两点之间，线段最短”可知，到A，B两村的路程最短的点在AB上任一点都可，这点还要在直线l上，所以就是AB与l的交点．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

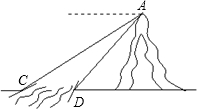    精英家教网如图，小山脚下有一条小河，从山顶A处测得河对岸点C的俯角为30°，测得岸边
    点D的俯角为45°，又知河宽CD为50米．现需从山顶A到河岸点C拉一条笔直的缆绳AC，求缆绳AC的长．（精确到0.1米，
    		2
    ≈1.41    ，
    		3
    ≈1.73    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    王林想用镜子测量一棵古松树的高，但因树旁有一条小河，不能测量镜子与树之间的距离，于是他两次利用镜子，如图，第一次他把镜子放在C点，人在F点正好在镜中看到树尖A；第二次他把镜子放在C′处，人在F′处正好看到树尖A．已知王林眼睛距地面1.7m，量得CC′为12m，CF为1.8m，C′F′为3.84m，求这棵古松树的高．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

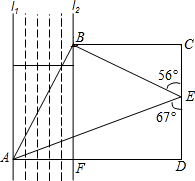    （2012•郑州模拟）如图所示，一条小河的两岸l1∥l2，和两岸各有一座建筑A和B，为测得A，B间的距离，小明从点B出发，沿垂直河岸l2的方向上选一点C，然后沿垂直于BC的直线行进了24米到达D，测得∠CDA=90°，取CD的中点E，测得∠BEC=56°，∠AED=67°，求A，B间的距离．（参考数据：sin56°≈
    4
    5
    tan56°≈
    3
    2
    sin67°≈
    14
    15
    tan67°≈
    7
    3
    262=676272=729）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    18世纪时，风景秀丽的小城哥尼斯堡中有一条小河，河的中间有两个小岛，河两岸与小岛之间共建有7座桥（图1）．当时小城的居民中流传着一道难题：“一个人怎样走才能不重复地走过所有7座桥，再回到出发点？”
    这就是数学史上著名的“7桥问题“，著名的数学家欧拉知道了“7桥问题“，他用四个点A、B、C、D分别表示小岛和河岸，用7条线表示7座桥（图2），于是，问题就成为“如何一笔画出图2中的图形？“欧拉经过研究发现，图2不能一笔画出．这就是说，找不到不重复地经过所有7座桥的路线．
    可以想象，凡是“一笔画“，一定有一个“起点“，一个“终点“，还有一些“过路点“，有一条进入过路点，必有一条线离开过路点．这样，与过路点相连的线必为偶数条，而与奇数条线相连的点，只能是起点和终点，这样的点的个数只能是
    0或2
    0或2
    个
    如果你还不能填上面的空，请你研究图3的四个图形，根据你的研究结果，把上面的空填上．
    在7桥问题中，如果允许你再架一座桥，能否不重复地一次走遍这8座桥？这座桥应建在何处？请你在图2中画出来．并回答有哪几种方式．

    查看答案和解析>>

    同步练习册答案