
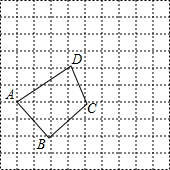
 如图,网格中的每一格的边长为1个单位长度,已知四边形ABCD的顶点均在网格的个点上.
如图,网格中的每一格的边长为1个单位长度,已知四边形ABCD的顶点均在网格的个点上. 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
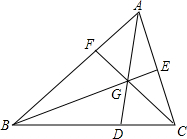 如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.
如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “抛掷一枚硬币,硬币落地时正面朝上”是随机事件 | |
| B. | “任意打开数学教科书八年级下册,正好是第50页”是不可能事件 | |
| C. | “把4个球放入三个抽屉中,其中必有一个抽屉中至少有2个球”是必然事件 | |
| D. | “在一个不透明的袋子中,有5个除颜色外完全一样的小球,其中2个红球,3个白球,从中任意摸出1个小球,正好是红球”是随机事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com