
 把正△ABO绕着点O,按顺时针方向旋转任意角度α得到△CDO,边CD与AB交于点H(如图).
把正△ABO绕着点O,按顺时针方向旋转任意角度α得到△CDO,边CD与AB交于点H(如图). 解:(1)HC=HB.
解:(1)HC=HB. ,
, ,
, -3,
-3, ,2
,2 -3).
-3).

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
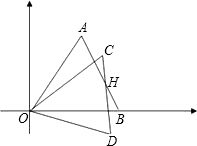 把正△ABO绕着点O,按顺时针方向旋转任意角度α得到△CDO,边CD与AB交于点H(如图).
把正△ABO绕着点O,按顺时针方向旋转任意角度α得到△CDO,边CD与AB交于点H(如图).查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷45(南阳初中 刘东旭 金凯)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com