
 如图,在一面靠墙的空地商用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
如图,在一面靠墙的空地商用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.分析 (1)根据面积等于长乘宽即可解决问题.自变量的取值范围可以根据不等式4x<24解决问题.
(2)①根据条件先确定自变量取值范围,再利用配方法,结合自变量取值范围,确定x取何值时面积最大.
②先求出-4x2+24x=20方程的解,再根据二次函数的图象以及自变量的取值范围,确定x的取值范围.
解答 解:(1)S=x(24-4x)=-4x2+24x(0<x<6)
(2)①S=-4x2+24x=-4(x-3)2+36
由$\left\{\begin{array}{l}{24-4x≤8}\\{24-4x>0}\end{array}\right.$,解得4≤x<6
当x=4时,花圃有最大面积为32
②令-4x2+24x=20时,解得x1=1,x2=5
∵墙的最大可用长度为8,即24-4x≤8
∴x≥4
∴4≤x≤5.
点评 本题考查二次函数的应用、一元二次方程的应用,解题的关键是学会构建二次函数解决实际问题,取最值注意自变量的取值范围,属于中考常考题型.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
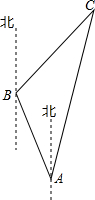 为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离($\sqrt{6}$≈2.45,结果保留到整数)
为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离($\sqrt{6}$≈2.45,结果保留到整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
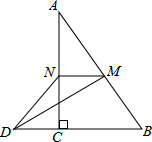 如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DM、DN、MN.若AB=6,则DN=3.
如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DM、DN、MN.若AB=6,则DN=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com