
【题目】(背景)如图(a),△ABC与△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
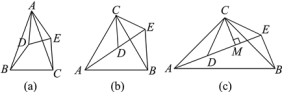
(探究)如图(b),△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为________;②线段BE与AD之间的数量关系是________.
(拓展)如图(c),△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②请直接写出线段CM,AE,BE之间的数量关系.
【答案】背景:见解析;探究:①60° ②BE=AD;拓展:(1)90°;(2)AE=BE+2CM
【解析】
背景:根据全等三角形的判定方法,判断出△BAD≌△CAE,即可判断出BD=CE;
探究:①根据△ACB和△DCE均为等边三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出∠BEC=∠ADC,进而判断出∠AEB的度数为60°即可;
②,由△ACD≌△BCE,即可判断出BE=AD;
拓展:①根据△ACB和△DCE均为等腰直角三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°即可;
②根据∠DCE=90°,CD=CE,CM⊥DE,可得CM=DM=EM,所以DE=DM+EM=2CM,据此判断出AE=BE+2CM即可.
背景:∵∠BAC=∠DAE=40°,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,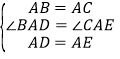 ,
,
∴△BAD≌△CAE,∴BD=CE;
探究:①∵△ACB和△DCE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∠CDE=∠CED=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,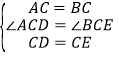 ,
,
∴△ACD≌△BCE,
∴∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180-60=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120-60=60°,
故答案为:60°;
②∵△ACD≌△BCE,
∴BE=AD,
故答案为:BE=AD;
拓展:①∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,CD=CE,∠CDE=∠CED=45°,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
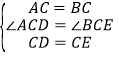 ,
,
∴△ACD≌△BCE,
∴AD=BE,∠ADC=∠BEC,
∵点A,D,E在同一直线上,
∴∠ADC=180°-∠CDE=180°-45°=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°;
②∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM,
又∵AD=BE,
∴AE=AD+DE=BE+2CM


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上,A、B两点表示的数a,b满足|a﹣6|+(b+12)2=0
(1)a= ,b= ;
(2)若小球M从A点向负半轴运动、小球N从B点向正半轴运动,两球同时出发,小球M运动的速度为每秒2个单位,当M运动到OB的中点时,N点也同时运动到OA的中点,则小球N的速度是每秒 个单位;
(3)若小球M、N保持(2)中的速度,分别从A、B两点同时出发,经过 秒后两个小球相距两个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,在△ABC中,已知∠ADE=∠B,∠1=∠2,FG⊥AB于点G.
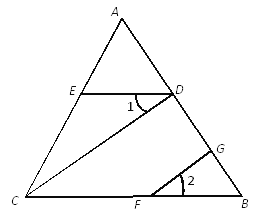
求证CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴ ( ),
∵ DE∥BC(已证),
∴ ( ),
又∵∠1=∠2(已知),
∴ ( ),
∴CD∥FG( ),
∴ (两直线平行同位角相等),
∵ FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
即∠CDB=∠FGB=90°,
∴CD⊥AB. (垂直的定义).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为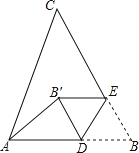
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com