
 如图,在△ABC中,∠A=50°,点O是△ABC三边垂直平分线的交点,则∠BOC=100°.
如图,在△ABC中,∠A=50°,点O是△ABC三边垂直平分线的交点,则∠BOC=100°. 分析 连接AO,根据线段垂直平分线上的点到线段两端点的距离相等看得到AO=BO=CO,根据等边对等角可得∠ABO=∠BAO,∠ACO=∠CAO,然后求出∠ABO+∠ACO+∠BAC,再根据三角形的内角和等于180°求出∠OBC+∠OCB,再次利用三角形的内角和定理求解即可.
解答 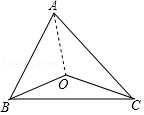 解:如图,连接AO,
解:如图,连接AO,
∵点O是△ABC三边垂直平分线的交点,
∴AO=BO=CO,
∴∠ABO=∠BAO,∠ACO=∠CAO,
∴∠ABO+∠ACO+∠BAC=2∠BAC=2×50°=100°,
在△ABC中,根据三角形的内角和定理得,∠OBC+∠OCB=180°-100°=80°,
在△OBC中,根据三角形的内角和定理得,∠BOC=180°-(∠OBC+∠OCB)=180°-80°=100°.
故答案为:100°.
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,三角形的内角和定理,熟记性质并作辅助线构造出等腰三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
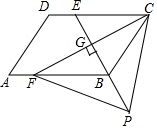 如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有①②③④.(填序号)
如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有①②③④.(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
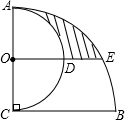 如图,AC⊥BC,AC=BC=6,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{AB}$.过点O作BC的平行线交两弧于D、E,则阴影部分的面积是$\frac{15}{4}$π-$\frac{9\sqrt{3}}{2}$.
如图,AC⊥BC,AC=BC=6,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{AB}$.过点O作BC的平行线交两弧于D、E,则阴影部分的面积是$\frac{15}{4}$π-$\frac{9\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
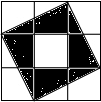 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是$\frac{4}{9}$.
小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是$\frac{4}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
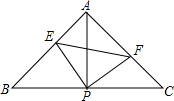 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.上述结论正确的有( )
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.上述结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com