
 正方形ABCD中,E、F分别在AD、DC上,∠ABE=∠CBF=15°,G是AD上另一点,且∠BGD=120°,连接EF、BG、FG、EF、BG交于点H,则下面结论:①DE=DF;②△BEF是等边三角形;③∠BGF=45°;④BG=EG+FG中,正确的是①②④(请填番号)
正方形ABCD中,E、F分别在AD、DC上,∠ABE=∠CBF=15°,G是AD上另一点,且∠BGD=120°,连接EF、BG、FG、EF、BG交于点H,则下面结论:①DE=DF;②△BEF是等边三角形;③∠BGF=45°;④BG=EG+FG中,正确的是①②④(请填番号) 分析 ①正确.由△BAE≌△BCF,推出AE=CF,即可证明.
②正确.由△BAE≌△BCF,推出BE=BF,再证明∠EBF=60°即可证明.
③错误.由△EHG∽△BHF,推出$\frac{EH}{BH}$=$\frac{HG}{HF}$,推出$\frac{EH}{HG}$=$\frac{BH}{HF}$又∠EHB=∠GHF,推出△EHB∽△GHF,即可推出∠BEH=∠BGF=60°.
④正确.只要证明△BFM≌△EFG,即可解决问题.
解答 证明:连接BD,在BG上取一点M,使得GM=GF.
∵四边形ABCD是正方形,
∴AB=CB=AD=CD,∠ABC=∠A=∠C=90°,∠ABD=∠CBD=45°,
在△BAE和△BCF中,
$\left\{\begin{array}{l}{∠ABE=∠CBF}\\{AB=CB}\\{∠A=∠C}\end{array}\right.$,
∴△BAE≌△BCF,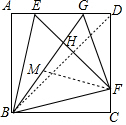
∴BE=BF,AE=CF,
∴DE=DF,故①正确,
∵∠ABE=∠CBF=15°,
∠EBF=60°,
∴△EBF是等边三角形,故②正确,
∵∠BGD=120°,
∴∠EGH=∠HFB=60°,
∵∠EHG=∠BHF,
∴△EHG∽△BHF,
∴$\frac{EH}{BH}$=$\frac{HG}{HF}$,
∴$\frac{EH}{HG}$=$\frac{BH}{HF}$,∵∠EHB=∠GHF,
∴△EHB∽△GHF,
∴∠BEH=∠BGF=60°,故③错误,
∵GM=GF,
∴△GMF是等边三角形,
∴FM=FG,∠MFG=∠BFE=60°,
∴∠BFM=∠EFG,∵BF=FE,
∴△BFM≌△EFG,
∴BM=EG,
∴GB=GM+BM=GF+EG,故④正确.
故答案为①②④.
点评 本题考查正方形的性质、全等三角形的判定和性质、等边三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (2,4) | B. | (2,3) | C. | (-1,6) | D. | (-$\frac{1}{2}$,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
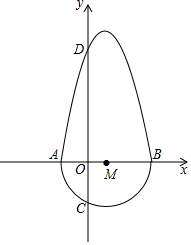 定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为3.
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
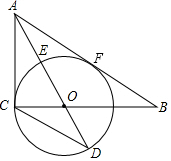 如图,Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
如图,Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com