
【题目】如图,在边长为2的正方形ABCD中,点E是边AD中点,点F在边CD上,且FE⊥BE,设BD与EF交于点G,则△DEG的面积是___

【答案】![]()
【解析】
过点G作GM⊥AD于M,先证明△ABE∽△DEF,利用相似比计算出DF=![]() ,再利用正方形的性质判断△DGM为等腰直角三角形得到DM=MG,设DM=x,则MG=x,EM=1-x,然后证明△EMG∽△EDF,则利用相似比可计算出GM,再利用三角形面积公式计算S△DEG即可.
,再利用正方形的性质判断△DGM为等腰直角三角形得到DM=MG,设DM=x,则MG=x,EM=1-x,然后证明△EMG∽△EDF,则利用相似比可计算出GM,再利用三角形面积公式计算S△DEG即可.
解:过点G作GM⊥AD于M,如图,
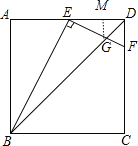
∵FE⊥BE,
∴∠AEB+∠DEF=90°,
而∠AEB+∠ABE=90°,
∴∠ABE=∠DEF,
而∠A=∠EDF=90°,
∴△ABE∽△DEF,
∴AB:DE=AE:DF,即2:1=1:DF,
∴DF=![]() ,
,
∵四边形ABCD为正方形,
∴∠ADB=45°,
∴△DGM为等腰直角三角形,
∴DM=MG,
设DM=x,则MG=x,EM=1-x,
∵MG∥DF,
∴△EMG∽△EDF,
∴MG:DF=EM:ED,即x:![]() =(1-x):1,解得x=
=(1-x):1,解得x=![]() ,
,
∴S△DEG=![]() ×1×
×1×![]() =
=![]() ,
,
故答案为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
“地球一小时”是世界自然基金会在2007年提出的一项倡议.号召个人、社区、企业和政府在每年3月最后一个星期六20时30分﹣21时30分熄灯一小时,旨在通过一个人人可为的活动,让全球民众共同携手关注气候变化,倡导低碳生活.中国内地去年和今年共有119个城市参加了此项活动,且今年参加活动的城市个数比去年的3倍少13个,问中国内地去年、今年分别有多少个城市参加了此项活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图1所示的程序,得到了如图y与x的函数图像,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图像于点P、Q,连接OP、OQ.则以下结论:①x<0 时,y=![]() ;②△OPQ的面积为定值;③x>0时,y随x的增大而增大;④MQ=2PM⑤∠POQ可以等于90°.其中正确结论序号是( )
;②△OPQ的面积为定值;③x>0时,y随x的增大而增大;④MQ=2PM⑤∠POQ可以等于90°.其中正确结论序号是( )
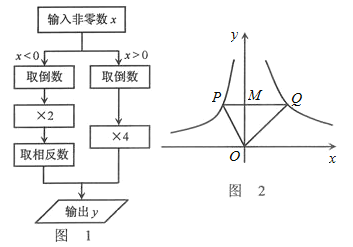
A.①②③B.②③④C.③④⑤D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,用直尺和圆规进行如下操作:
①以点A为圆心,以AD的长为半径画弧交BC于点E;
②连接AE,DE;
③作DF⊥AE于点F.
根据操作解答下列问题:
(1)线段DF与AB的数量关系是 .
(2)若∠ADF=60°,求∠CDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次暑假旅游中,小明在湖泊的游船上(A处),测得湖西岸的山峰(C处)和湖东岸的山峰(D处)的仰角都是45°,游船向东航行100米后到达B处,测得C、D两处的仰角分别为30°,60°,试求出C、D两座山的高度为多少米?(结果保留整数)(![]() ≈1.73)
≈1.73)
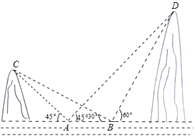
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商贩出售一批进价为l元的钥匙扣,在销售过程中发现钥匙扣的日销售单价x(元)与日销售量y(个)之间有如下关系:

(1)根据表中数据在平面直角坐标系中,描出实数对(x,y)对应的点;
(2)猜想并确定y与x的关系式,并在直角坐标系中画出x>0时的图像;
(3)设销售钥匙扣的利润为T元,试求出T与x之间的函数关系式:若商贩在钥匙扣售价不超过8元的前提下要获得最大利润,试求销售价x和最大利润T.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 是反比例函数.
是反比例函数.
(1)求m的值;
(2)指出该函数图象所在的象限,在每个象限内,y随x的增大如何变化?
(3)判断点(![]() ,2)是否在这个函数的图象上.
,2)是否在这个函数的图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com