
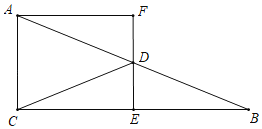
【题目】Rt△ABC中,∠ACB=90°,点D是AB中点,连CD,过点D作DE⊥BC于E,过A作AF⊥ED的延长线于F.
(1)若∠B=25°,求∠ADC的度数;
(2)求证:DF=DE.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的盒子中,装有2个白球和1个红球,这些球除颜色外其余都相同.
(1)你同意下列说法吗?请说明理由.
①搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球这两个事件是等可能的.
②如果将摸出的第一个球放回搅匀后再摸出第二个球,两次摸球就可能出现3种结果,即“都是红球”、“都是白球”、“一红一白”.这三个事件发生的概率相等.
(2)搅匀后从中任意摸出一个球,要使摸出红球的概率为![]() ,应如何添加红球?
,应如何添加红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=3x2+bx+c与直线y=﹣1只有一个公共点M,与平行于x轴的直线l交此抛物线A,B两点若AB=4,则点M到直线l的距离为( )
A.11B.12C.![]() D.13
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
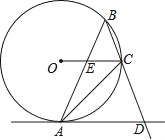
【题目】如图⊙O是△ABC的外接圆,∠ABC=45°,延长BC于D,连接AD,使得AD∥OC,AB交OC于E.
(1)求证:AD与⊙O相切;
(2)若AE=2![]() ,CE=2.求⊙O的半径和AB的长度.
,CE=2.求⊙O的半径和AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
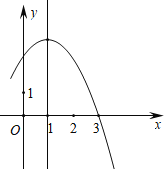
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(3,0),且对称轴为直线x=1.下列说法,其中正确的是( )
①abc<0
②b2﹣4ac>0;
③a﹣b+c<0;
④b﹣c>2a
A.①②B.①③④C.②④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+
x2+![]() x+6与x轴相交A,B两点,与y轴相交于点C.
x+6与x轴相交A,B两点,与y轴相交于点C.
(1)若点E为线段BC上一动点,过点E作x轴的垂线与抛物线交于点P,垂足为F,当PE﹣2EF取得最大值时,在抛物线y的对称轴上找点M,在x轴上找点N,使得PM+MN+![]() NB的和最小,若存在,求出该最小值及点N的坐标;若不存在,请说明理由.
NB的和最小,若存在,求出该最小值及点N的坐标;若不存在,请说明理由.
(2)在(1)的条件下,若点P′为点P关于x轴的对称点,将抛物线y沿射线BP′的方向平移得到新的抛物线y′,当y′经过点A时停止平移,将△BCN沿CN边翻折,点B的对应点为点B′,B′C与x轴交于点K,若抛物线y′的对称轴上有点R,在平画内有点S,是否存在点R、S使得以K、B′、R、S为顶点的四边形是菱形,若存在,直接写出点S的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花园小区有一朝向为正南方向的居民楼(如图),该居民楼的一楼是高4米的小区商场,商场以上是居民住房.在该楼的前面16米处要盖一栋高18米的办公楼.当冬季正午的阳光与水平线的夹角为![]() 时,问:
时,问:
(1)商场以上的居民住房采光是否有影响,为什么?
(2)若要使商场采光不受影响,两楼应相距多少 米?(结果保留一位小数)
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
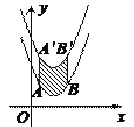
【题目】如图,将二次函数y=![]() (x-2)2+1的图像沿y轴向上平移得到一条新的二次函数图像,其中A(1,m),B(4,n)平移后对应点分别是A′、B′,若曲线AB所扫过的面积为12(图中阴影部分),则新的二次函数对应的函数表达是__________________.
(x-2)2+1的图像沿y轴向上平移得到一条新的二次函数图像,其中A(1,m),B(4,n)平移后对应点分别是A′、B′,若曲线AB所扫过的面积为12(图中阴影部分),则新的二次函数对应的函数表达是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )
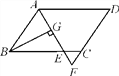
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com