
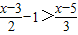
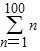 ,这里“Σ”是求和符号.
,这里“Σ”是求和符号.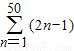 ;又如:“13+23+33+43+53+63+73+83+93+103”可表示为
;又如:“13+23+33+43+53+63+73+83+93+103”可表示为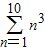 .
.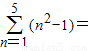 ______(填写最后的计算结果).
______(填写最后的计算结果). 1+3+8+15+24,计算可得答案.
1+3+8+15+24,计算可得答案.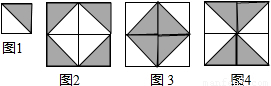
 .(1分)
.(1分)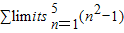 =0+3+8+15+24=50.(1分)
=0+3+8+15+24=50.(1分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 (2003•无锡)某商场为提高彩电销售人员的积极性,制定了新的工资分配方案.方案规定:每位销售人员的工资总额=基本工资+奖励工资.每位销售人员的月销售定额为10000元,在销售定额内,得基本工资200元;超过销售定额,超过部分的销售额按相应比例作为奖励工资,奖励工资发放比例如表1所示.
(2003•无锡)某商场为提高彩电销售人员的积极性,制定了新的工资分配方案.方案规定:每位销售人员的工资总额=基本工资+奖励工资.每位销售人员的月销售定额为10000元,在销售定额内,得基本工资200元;超过销售定额,超过部分的销售额按相应比例作为奖励工资,奖励工资发放比例如表1所示.查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《二次函数》(03)(解析版) 题型:解答题
 ,抛物线的顶点为点P,是否存在这样的抛物线,使得△PAB的外接圆半径为
,抛物线的顶点为点P,是否存在这样的抛物线,使得△PAB的外接圆半径为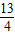 ?若存在,求出这样的抛物线的解析式;若不存在,请说明理由.
?若存在,求出这样的抛物线的解析式;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2003年江苏省无锡市中考数学试卷(解析版) 题型:解答题
 ,抛物线的顶点为点P,是否存在这样的抛物线,使得△PAB的外接圆半径为
,抛物线的顶点为点P,是否存在这样的抛物线,使得△PAB的外接圆半径为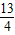 ?若存在,求出这样的抛物线的解析式;若不存在,请说明理由.
?若存在,求出这样的抛物线的解析式;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《数据分析》(02)(解析版) 题型:填空题
| 捐款数(元) | 1 | 2 | 3 | 4 |
| 捐款人数 | 2 | 24 | 21 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com