
【题目】甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的![]() 倍,4分钟两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙二人的速度及环形场地的周长
倍,4分钟两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙二人的速度及环形场地的周长![]() 列方程
列方程![]() 组
组![]() 求解
求解![]()
【答案】乙的速度为150米![]() 分,甲的速度为375米
分,甲的速度为375米![]() 分,环形场地的周长为900米.
分,环形场地的周长为900米.
【解析】
试题由“4分钟后两人首次相遇”,可知跑步4分钟后,甲比乙多跑一圈,即可得到相等关系;设乙的速度为x米/分,则甲的速度是2.5x米/分,根据等量关系列出方程进行求解,即可得到乙和甲的速度;然后由乙跑了4分钟之后还差300米便可跑完一整圈,即可求出场地的周长.
解:设乙的速度为x m/min,
则甲的速度为2.5x m/min.
由题意,得2.5x×4-4x=4x+300.
解得x=150.
所以2.5x=2.5×150=375,
4x+300=4×150+300=900.
答:甲、乙两人的速度分别为375 m/min.


科目:初中数学 来源: 题型:
【题目】如图在△AFD和△CEB中,点A、E、F、C在同一条直线上.有下面四个论断:
(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD∥BC.
请用其中三个作为条件,余下一个作为结论,进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品经销店欲购进A、B两种纪念品,用320元购进的A种纪念品与用400元购进的B种纪念品的数量相同,每件B种纪念品的进价比A种纪念品的进价贵10元.
(1)求A、B两种纪念品每件的进价分别为多少?
(2)若该商店A种纪念品每件售价45元,B种纪念品每件售价60元,这两种纪念品共购进200件,这两种纪念品全部售出后总获利不低于1600元,求A种纪念品最多购进多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
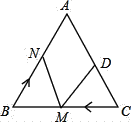
【题目】如图,在等边![]() 中,
中,![]() 厘米,
厘米,![]() 厘米.如果点
厘米.如果点![]() 以
以![]() 厘米/秒的速度运动,如果点
厘米/秒的速度运动,如果点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动,点
运动,点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.它们同时出发,若点
点运动.它们同时出发,若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等.
的运动速度相等.
(1)经过![]() 秒后,
秒后,![]() 和
和![]() 是否全等?请说明理由.
是否全等?请说明理由.
(2)当两点的运动时间为多少时,![]() 是一个直角三角形?
是一个直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC=10 cm,AB=12 cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2 cm,设运动时间为![]() 秒.
秒.
(1)求CD的长;
(2)当![]() 为何值时,△ADP是直角三角形?
为何值时,△ADP是直角三角形?
(3)直接写出:当![]() 为何值时,△ADP是等腰三角形?
为何值时,△ADP是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系 ;
(2)如图2,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;
(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泰兴市为进一步改善生态环境决定对街道进行绿化建设,为此准备购进甲、乙两种树木、已知甲种树木的单价为![]() 元,乙种树木的单价为
元,乙种树木的单价为![]() 元.
元.
(1)若![]() 街道购买甲、乙两种树木共花费
街道购买甲、乙两种树木共花费![]() 元,其中,乙种树木是甲种树木的一半多
元,其中,乙种树木是甲种树木的一半多![]() 棵,请求出该街道购买的甲、乙两种树木各多少棵;
棵,请求出该街道购买的甲、乙两种树木各多少棵;
(2)相关资料表明:甲种树木的成活率为![]() ,乙种树木的成活率为
,乙种树木的成活率为![]() .现
.现![]() 街道购买甲、乙两种树木共
街道购买甲、乙两种树木共![]() 棵,为了使这批树木的总成活率不低于
棵,为了使这批树木的总成活率不低于![]() ,则甲种树木至多购买多少棵?
,则甲种树木至多购买多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
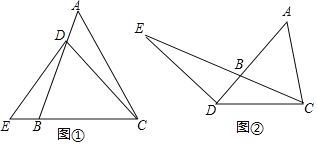
【题目】已知:![]() 是等腰三角形,其底边是BC,点D在直线AB上,E是直线BC上一点,且
是等腰三角形,其底边是BC,点D在直线AB上,E是直线BC上一点,且![]() .
.
![]() 如图
如图![]() ,点D在线段AB上,若
,点D在线段AB上,若![]() ,判断EB与AD的数量关系
,判断EB与AD的数量关系![]() 不必证明
不必证明![]() ;
;
![]() 若点D在线段AB的延长线上,其它条件不变
若点D在线段AB的延长线上,其它条件不变![]() 如图
如图![]() ,
,![]() 的结论是否成立,请说明理由;
的结论是否成立,请说明理由;
![]() 若
若![]() ,其它条件不变,EB与AD的数量关系是怎样的?
,其它条件不变,EB与AD的数量关系是怎样的?![]() 用含有
用含有![]() 的关系式直接写出结论,不要求写解答过程
的关系式直接写出结论,不要求写解答过程![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com