
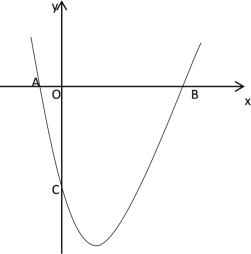
【题目】如图:已知抛物线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,此抛物线的对称轴为直线
,此抛物线的对称轴为直线![]() .
.
![]() 求出此抛物线的解析式;
求出此抛物线的解析式;
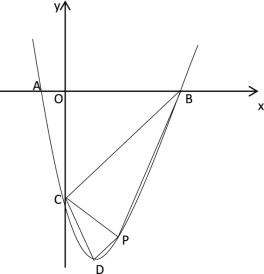
![]() 如图 1,抛物线的顶点为点
如图 1,抛物线的顶点为点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的一点(异于点
下方抛物线上的一点(异于点![]() ),当
),当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
![]() 在
在![]() 的条件下,将抛物线沿射线
的条件下,将抛物线沿射线![]() 方向平移,点
方向平移,点![]() 的对应点为
的对应点为![]() ,在抛物线平移的过程中,若
,在抛物线平移的过程中,若![]() ,请直接写出此时平移后的抛物线解析式
,请直接写出此时平移后的抛物线解析式

【答案】(1)![]() ;(2)
;(2)![]() ;
;![]() 新抛物线解析式为新抛物线解析式为
新抛物线解析式为新抛物线解析式为![]() 或
或![]() .
.
【解析】
(1)根据抛物线的对称轴和A、C两点的坐标即可求出结论;
(2)先求出点D的坐标,过点![]() 作直线
作直线![]() 交抛物线于点
交抛物线于点![]() ,根据平行线的距离处处相等可得此时
,根据平行线的距离处处相等可得此时![]() ,利用待定系数法求出直线BC的解析式,然后求出直线DP的解析式,然后联立方程即可求出点P的坐标;
,利用待定系数法求出直线BC的解析式,然后求出直线DP的解析式,然后联立方程即可求出点P的坐标;
(3)根据点P′与BC的位置关系分类讨论,分别画出对应的图形,利用待定系数法求出各个直线的解析式,联立方程即可求出点P′的坐标,从而求出平移方式,然后即可求出新抛物线的解析式.
![]() 由题抛物线对称轴为直线
由题抛物线对称轴为直线 ![]() 且过点
且过点![]()
得 ,
,
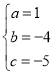
![]() 抛物线解析式为
抛物线解析式为![]()
![]() 由题抛物线的顶点
由题抛物线的顶点![]()
过点![]() 作直线
作直线![]() 交抛物线于点
交抛物线于点![]() ,根据平行线的距离处处相等可得此时
,根据平行线的距离处处相等可得此时![]()
利用对称性可知点B的坐标为(5,0)
设直线BC的解析式为y=kx+d
将![]() 代入,得
代入,得
![]()
解得:![]()
![]()
设直线DP的解析式为y=x+e
将点D的坐标代入,得
![]()
解得:e=-11
![]()
则![]()
解得: (舍去),
(舍去),
![]()
![]() 若点P′在BC右侧时,作∠ECB=∠PBC交BP与点E,过点P作PP′∥DC交EC于P′,连接OE,如下图所示,易知点P′符合条件
若点P′在BC右侧时,作∠ECB=∠PBC交BP与点E,过点P作PP′∥DC交EC于P′,连接OE,如下图所示,易知点P′符合条件

∴EB=EC
∵OB=OC=5,
∴OE垂直平分BC
∴∠BOE=![]() ∠BOC=45°,即点E在∠BOC的角平分线上
∠BOC=45°,即点E在∠BOC的角平分线上
∴可设E点的坐标为(m,-m)
设直线BP的解析式为y=k1x+b1
将点B、P的坐标代入,可得
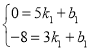
解得:
∴直线BP的解析式为y=4x-20
将点E的坐标代入可得-m=4m-20
解得:m=4
∴点E的坐标为(4,-4)
同理可得CE的解析式为y=![]() x-5
x-5
直线CD的解析式为y=-2x-5
直线PP′的解析式为y=-2x-2
联立
解得:
∴点P′(![]() )
)
∴点![]() 到点P′(
到点P′(![]() )的平移方式为先向左平移
)的平移方式为先向左平移![]() 个单位长度,在向上平移
个单位长度,在向上平移![]() 个单位长度
个单位长度
原抛物线的解析式为![]()
∴新抛物线解析式为![]()
若点P′在BC左侧时,作CP′∥BP,PP′∥CD,CP′与PP′交于点P′,如下图所示,此时![]()

由上可知:直线BP的解析式为y=4x-20,可得直线CP′的解析式为y=4x-5
直线PP′的解析式为y=-2x-2
联立![]()
解得:
∴点P′(![]() )
)
∴点![]() 到点P′(
到点P′(![]() )的平移方式为先向左平移
)的平移方式为先向左平移![]() 个单位长度,在向上平移5个单位长度
个单位长度,在向上平移5个单位长度
原抛物线的解析式为![]()
∴新抛物线解析式为![]()
综上:新抛物线解析式为![]() 或
或![]()


科目:初中数学 来源: 题型:
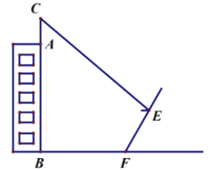
【题目】如图,某校有一教学楼![]() ,其上有一避雷针
,其上有一避雷针![]() 为
为![]() 米,教学楼后面有一小山,其坡度为
米,教学楼后面有一小山,其坡度为![]() 山坡上有一休息亭
山坡上有一休息亭![]() 供爬山人员休息,测得山坡脚
供爬山人员休息,测得山坡脚![]() 与教学搂的水平距离
与教学搂的水平距离![]() 为
为![]() 米,与休息亭的距离
米,与休息亭的距离![]() 为
为![]() 米,从休息亭
米,从休息亭![]() 测得教学楼上避雷针顶点
测得教学楼上避雷针顶点![]() 的仰角为
的仰角为![]() ,求教学搂
,求教学搂![]() 的高度.(结果保留根号)(注:坡度
的高度.(结果保留根号)(注:坡度![]() 是指坡面的铅直高度与水平宽度的比)
是指坡面的铅直高度与水平宽度的比)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
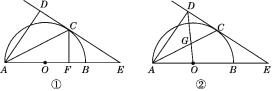
(1)求证:AC平分∠DAB;
(2)若AB=6,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() =
=![]() ,求cosE的值.
,求cosE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
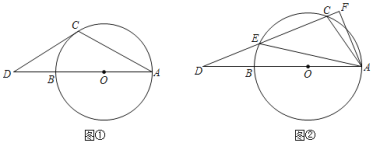
【题目】已知AB为⊙O的直径,点C为⊙O上一点,点D为AB延长线一点,连接AC.
(Ⅰ)如图①,OB=BD,若DC与⊙O相切,求∠D和∠A的大小;
(Ⅱ)如图②,CD与⊙O交于点E,AF⊥CD于点F连接AE,若∠EAB=18°,求∠FAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
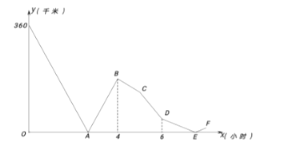
【题目】快慢两车分别从相距![]() 千米的甲、乙两地同时出发,匀速行驶,途中慢车因故障停留
千米的甲、乙两地同时出发,匀速行驶,途中慢车因故障停留![]() 小时,然后 以原速度的
小时,然后 以原速度的![]() 倍继续向甲地行驶,到达甲地后停止行驶;快车匀速到达乙地后,立即按原路原速返回甲 地(快车掉头时间忽略不计),并且比慢车提前
倍继续向甲地行驶,到达甲地后停止行驶;快车匀速到达乙地后,立即按原路原速返回甲 地(快车掉头时间忽略不计),并且比慢车提前![]() 分钟到达甲地,快慢两车之间的距离
分钟到达甲地,快慢两车之间的距离![]() (千米)与快 车行驶时间
(千米)与快 车行驶时间![]() (小时)之间的函数图象如图所示.则当两车第二次相遇时,两车距甲地还有________千米.
(小时)之间的函数图象如图所示.则当两车第二次相遇时,两车距甲地还有________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是线段AB上的一点,AB=6cm,O是AB外一定点.连接OP,将OP绕点O顺时针旋转120°得OQ,连接PQ,AQ.
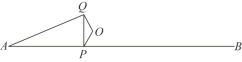
小明根据学习函数的经验,对线段AP,PQ,AQ的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,PQ,AQ的长度(单位:cm)的几组值,如下表:
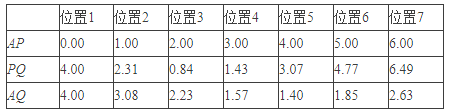
在AP,PQ,AQ的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
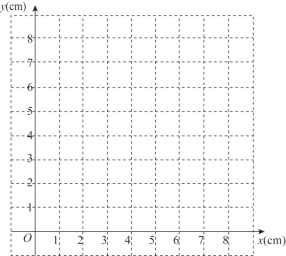
(3)结合函数图象,解决问题:当AQ=PQ时,线段AP的长度约为________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的
5个主题进行了抽样调查(每位同学只选取最关注的一个),根据调查结果绘制了两幅不完
整的统计图,根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整;
(3)在扇形统计图中“进取”部分扇形的圆心角是 度;
(4)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“感恩”的人数.
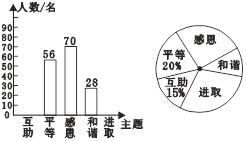
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l:
中,直线l:![]() 与直线
与直线![]() ,直线
,直线![]() 分别交于点A,B,直线
分别交于点A,B,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,结合函数图象,求区域
时,结合函数图象,求区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内没有整点,直接写出
内没有整点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com