
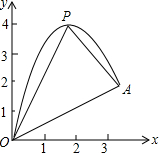
 如图,一小球从斜坡O点抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y=$\frac{1}{2}$x刻画,小球的落点是A.
如图,一小球从斜坡O点抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y=$\frac{1}{2}$x刻画,小球的落点是A.分析 (1)由题意可知点A是一次函数y=$\frac{1}{2}$x与二次函数y=-x2+4x的交点,从而可以解答本题;
(2)根据题意可以求得点P的坐标,从而可以求得△POA的面积.
解答 解:(1)$\left\{\begin{array}{l}{y=-{x}^{2}+4x}\\{y=\frac{1}{2}x}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{7}{2}}\\{{y}_{2}=\frac{7}{4}}\end{array}\right.$,
∴点A的坐标为($\frac{7}{2}$,$\frac{7}{4}$);
(2)∵y=-x2+4x=-(x-2)2+4,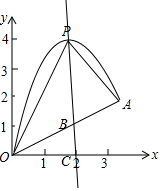
∴点P的坐标为(2,4),
作PC⊥x轴于点C交OA于点B,
将x=2代入y=$\frac{1}{2}$x,得y=$\frac{1}{2}×2$=1,
∴点B的坐标为(2,1),
∴PB=4-1=3,
∴S△POA=S△POB+S△PAB=$\frac{3×2}{2}+\frac{3×\frac{3}{2}}{2}$=$\frac{21}{4}$.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在+0.1的右边 | B. | 在-2的左边 | C. | 在原点与-$\frac{6}{5}$之间 | D. | 在-$\frac{4}{3}$的左边 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )| A. | 点C | B. | 点B | C. | 点A | D. | 点D |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -62=-36 | B. | -$\frac{1}{2}$-$\frac{1}{2}$=0 | C. | -3+(-2)=6 | D. | (-1)100+(-1)1000=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-3x2+2 | B. | y=-3x2-2 | C. | y=-3(x+2)2 | D. | y=-3(x-2)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com