
 如图,矩形ABCD中,AB=3,BC=4,点P在射线BC上运动,点P和点P′关于BD对称,当P′、P、D三点共线时运动停止,连接DP′、DP.设BP=x.
如图,矩形ABCD中,AB=3,BC=4,点P在射线BC上运动,点P和点P′关于BD对称,当P′、P、D三点共线时运动停止,连接DP′、DP.设BP=x.分析 (1)如图1所示:首先证明BP=BP′=P′D=x,则AP′=4-x.然后在Rt△AP′B中,依据勾股定理列方程求解即可;
(2)当点P′在矩形的内部时S△PBD=S△P′BD,然后依据S=S△PBD+S△P′BD=2S△PBD求解即可;当点P′在矩形的外部,点P在BC上时,由S=S△BDE+S△BDP求解即可;当点P在BC的延长线上时,由S=S△BDE+S△BDC求解即可.
解答 解:(1)如图1所示: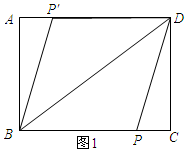
∵点P′与点P关于BD对称,
∴∠PBD=∠P′BD,BP=BP′.
∵AD∥BC,
∴∠PBD=∠ADB.
∴∠P′DB=∠P′BD,
∴P′D=P′B.
设BP=x,则BP′=P′D=x,AP′=4-x.
在Rt△AP′B中,依据勾股定理可知:32+(4-x)2=x2.
解得:x=$\frac{25}{8}$.
∴当x=$\frac{25}{8}$时,P′落在AD上;
(2)如图2所示: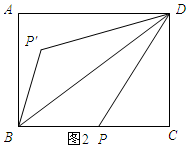
∵点P′与点P关于BD对称,
∴S△PBD=S△P′BD.
∴S=S△PBD+S△P′BD=2S△PBD=2×$\frac{1}{2}$BP•DC=3x(0≤x<$\frac{25}{8}$).
如图3所示:
由(1)可知:DE=$\frac{25}{8}$.
∴S△BDE=$\frac{1}{2}$DE•AB=$\frac{1}{2}$×$\frac{25}{8}$×3=$\frac{75}{16}$.
S△BDP=$\frac{1}{2}$BP•DC=$\frac{3}{2}$x.
∴S=S△BDE+S△BDP=$\frac{3}{2}$x+$\frac{75}{16}$($\frac{25}{8}$≤x<4).
如图4所示: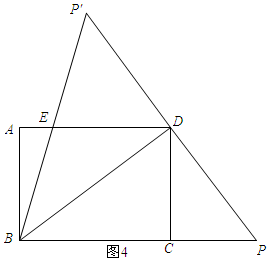
S=S△BDE+S△BDC=$\frac{75}{16}$+$\frac{1}{2}$×4×3=$\frac{171}{16}$.
在Rt△BCD中,依据勾股定理可知:BD=5.
∵当P′、P、D三点共线时运动停止,
∴点P′、D、P共线.
∵点P′与点P关于BD对称,
∴DP′=DP,BP′=BP,
∴BD⊥P′P.
∵∠DBC=∠DBP,∠DCB=∠BDP,
∴△BCD∽△BDP.
∴BP=$\frac{B{D}^{2}}{BC}$=$\frac{25}{4}$.
∴当4≤x≤$\frac{25}{4}$时,S=$\frac{171}{16}$.
综上所述,S与x的函数关系式为:S=$\left\{\begin{array}{l}{3x(0≤x<\frac{25}{8})}\\{\frac{3}{2}x+\frac{75}{16}(\frac{28}{5}≤x<4)}\\{\frac{171}{16}(4≤x≤\frac{25}{4})}\end{array}\right.$.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了矩形的性质、翻折的性质、勾股定理、相似三角形的性质和判定、三角形的面积公式,分类讨论是解题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-2=-2 | B. | 2-2=-$\frac{1}{4}$ | C. | (-2)-1=-$\frac{1}{2}$ | D. | (-$\frac{1}{2}$)-1=-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
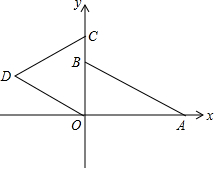 如图,Rt△OAB在平面直角坐标系中,点A在x轴的正半轴上,点B在y轴的正半轴上,且OA=3,OB=$\sqrt{3}$,边长为$\frac{3\sqrt{3}}{2}$的等边三角形OCD的一边OC在y轴的正半轴上,点D位于第二象限内.若等边三角形OCD以每秒1个单位的速度沿x轴的正方向运动,点D运动到y轴上则停止运动;设点O运动的对应点为点E,ED与y轴的交点为F,CD与y轴和AB的交点分别为H,G,CE与AB的交点为M,设△OCD运动的时间为t秒,△ECD与△OAB重叠部分的面积为S.
如图,Rt△OAB在平面直角坐标系中,点A在x轴的正半轴上,点B在y轴的正半轴上,且OA=3,OB=$\sqrt{3}$,边长为$\frac{3\sqrt{3}}{2}$的等边三角形OCD的一边OC在y轴的正半轴上,点D位于第二象限内.若等边三角形OCD以每秒1个单位的速度沿x轴的正方向运动,点D运动到y轴上则停止运动;设点O运动的对应点为点E,ED与y轴的交点为F,CD与y轴和AB的交点分别为H,G,CE与AB的交点为M,设△OCD运动的时间为t秒,△ECD与△OAB重叠部分的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com